题目内容
 如图,△BDE是等边三角形,∠BDC=30°,∠ABD=∠ADB=15°,∠CBD=45°.求证:△ABC是等边三角形.
如图,△BDE是等边三角形,∠BDC=30°,∠ABD=∠ADB=15°,∠CBD=45°.求证:△ABC是等边三角形.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:如图,连接EA.通过证明△BEA≌△BDC可以得到AB=BC,再根据“有一内角为60度的等腰三角形为等边三角形”证得结论.
解答: 证明:如图,连接EA.
证明:如图,连接EA.
∵△BDE是等边三角形,
∵BE=DE,∠EBD=∠EDB=60°,
又∵∠ABD=∠ADB=15°,
∴AB=AD,∠EBA=∠EDA=45°,
在△BEA与△DEA中,
,
∴△BEA≌△DEA(SAS),
∴∠BEA=∠DEA=30°.
∴∠BEA=∠BDC=30°.
在△BEA与△BDC中,
,
∴△BEA≌△BDC(ASA),
∴AB=CB.
又∵∠ABC=∠BCD+∠ABD=60°,
∴△ABC是等边三角形.
 证明:如图,连接EA.
证明:如图,连接EA.∵△BDE是等边三角形,
∵BE=DE,∠EBD=∠EDB=60°,
又∵∠ABD=∠ADB=15°,
∴AB=AD,∠EBA=∠EDA=45°,
在△BEA与△DEA中,
|
∴△BEA≌△DEA(SAS),
∴∠BEA=∠DEA=30°.
∴∠BEA=∠BDC=30°.
在△BEA与△BDC中,
|
∴△BEA≌△BDC(ASA),
∴AB=CB.
又∵∠ABC=∠BCD+∠ABD=60°,
∴△ABC是等边三角形.
点评:本题考查了全等三角形的判定与性质,等边三角形的判定.证明EA平分∠BED时,也可以通过作BD边上的垂线来证明EA是BD边上垂线上的两点,利用等腰三角形的“三线合一”的性质来推知.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图的坐标平面上有一正五边形ABCDE,其中C、D两点坐标分别为(1,0)、(2,0).若在没有滑动的情况下,将此正五边形沿着x轴向右滚动,则滚动过程中,下列哪个点会经过点(76,0)?( )
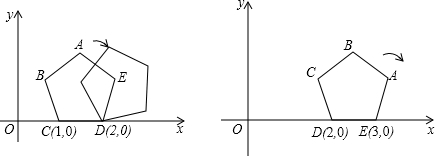

| A、A | B、B | C、C | D、D |
 如图,AB=DB,∠DBA=∠EBC,添加下列条件仍不能判定△ABC≌△DBE的是( )
如图,AB=DB,∠DBA=∠EBC,添加下列条件仍不能判定△ABC≌△DBE的是( )| A、BC=BE |
| B、AC=DE |
| C、∠A=∠D |
| D、∠C=∠E |
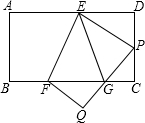 已知矩形纸片ABCD中,AD=6,CD=4,将纸片折叠,使点A落在CD边上点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
已知矩形纸片ABCD中,AD=6,CD=4,将纸片折叠,使点A落在CD边上点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.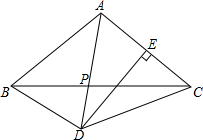 如图,在△ABC中,AB=AC,DE垂直平分AC,且∠CBD=30°,连接BD
如图,在△ABC中,AB=AC,DE垂直平分AC,且∠CBD=30°,连接BD