题目内容
6.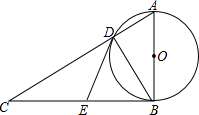 如图,在⊙O中,AB为直径,BC为⊙O的切线,D为⊙O上一点,AD的延长线与切线BC交于点C,E是BC的中点,连接DE,BD.
如图,在⊙O中,AB为直径,BC为⊙O的切线,D为⊙O上一点,AD的延长线与切线BC交于点C,E是BC的中点,连接DE,BD.(1)求证:DE是⊙O的切线;
(2)若tanC=$\frac{1}{2}$,DE=x,△ABD的面积为y,试求y与x之间的函数关系式.
分析 (1)根据圆周角定理得出BD⊥AC,然后根据直角三角形斜边中线的性质得出DE=BE,根据等边对等角得出∠EBD=∠EDB,然后根据等腰三角形的性质和切线的性质即可证得OD⊥DE,从而证得DE是⊙O的切线;
(2)根据直角三角形斜边中线的性质得出BC=2x,然后根据已知和勾股定理求得BD,进而求得AD,从而根据三角形面积公式求得y与x之间的函数关系式.
解答 (1)证明:∵AB为直径,
∴BD⊥AC,
∵E是BC的中点,
∴DE=BE,
∴∠EBD=∠EDB,
∵BC为⊙O的切线,
∴∠ABE=90°,
∴∠EBD+∠ABD=90°,
连接OD,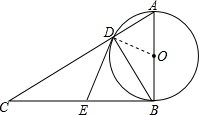 ∵OD=OB,
∵OD=OB,
∴∠ABD=∠ODB,
∴∠EDB+∠ODB=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)∵DE=x,
∴BC=2x,
∵tanC=$\frac{1}{2}$,
∴$\frac{BD}{CD}$=$\frac{1}{2}$,
∴CD=2BD,
∵CD2+BD2=BC2,
∴(2BD)2+BD2=4x2,
∴BD=$\frac{2\sqrt{5}}{5}$x,
∵∠ADB=∠ABC=90°,
∴∠C=∠ABD,
∴tan∠ABD=$\frac{AD}{BD}$=$\frac{1}{2}$,
∴AD=$\frac{\sqrt{5}}{5}$x,
∴y=$\frac{1}{2}$AD•BD=$\frac{1}{2}$×$\frac{\sqrt{5}}{5}$x•$\frac{2\sqrt{5}}{5}$x=x2,
即y=x2.
点评 本题考查了切线的判定和性质,圆周角定理的应用,勾股定理的应用,直角三角形斜边中线的性质等,证明某一线段是圆的切线时,一般情况下是连接切点与圆心,通过证明该半径垂直于这一线段来判定切线.

练习册系列答案
相关题目
16. 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )| A. | $({\sqrt{2}-1})a$ | B. | $\frac{{\sqrt{2}-1}}{2}a$ | C. | $\frac{{2-\sqrt{2}}}{4}a$ | D. | $({2-\sqrt{2}})a$ |
1.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如表:
经检查,发现表格中恰好有一组数据计算错误,错误的那组数据的序号是( )
| 序号 | ① | ② | ③ | ④ | ⑤ |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 8 | 3 | 0 | 1 | 0 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
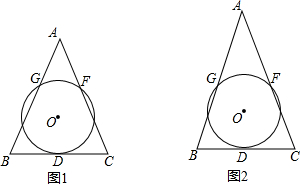
 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,过点D作DF∥BE交AC于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点E,过点D作DF∥BE交AC于点F.