题目内容
19. 如图,在△ABC中,AB=AC,D是BA延长线上的一点,AM是∠DAC的平分线.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,AM是∠DAC的平分线.(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法);
①作AC的中点 E.
②连接BE并延长交AM于点F;
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.
分析 (1)①作线段AC的垂直平分线交AC于点E即可;
②连接BE并延长交AM于点F即可;
(2)利用平行线的判断得出AF∥BC,再利用全等三角形的判定得出△AEF≌△CEB(ASA),进而得出AF=BC.
解答 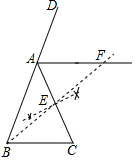 解:(1)①如图,点E即为所求;
解:(1)①如图,点E即为所求;
②如图,点F即为所求;
(2)AF∥BC且AF=BC.
理由如下:∵AB=AC,
∴∠ABC=∠C,
∴∠DAC=∠ABC+∠C=2∠C.
由作图可知:∠DAC=2∠FAC,
∴∠C=∠FAC,
∴AF∥BC.
∵E是AC的中点,
∴AE=CE.
在△AEF和△CEB中,
∵$\left\{\begin{array}{l}{∠FAE=∠ECB}\\{AE=EC}\\{∠AEF=∠CEB}\end{array}\right.$,
∴△AEF≌△CEB(ASA),
∴AF=BC.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法及全等三角形的判定与性质是解答此题的关键.

练习册系列答案
相关题目
14.一个等腰三角形的两边长分别是3和7,则它的周长为( )
| A. | 13 | B. | 15 | C. | 17 | D. | 13或17 |
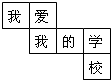 如图,该图形经过折叠可以围成一个正方体,折叠完成以后,则与“爱”字相对的字是“校”.
如图,该图形经过折叠可以围成一个正方体,折叠完成以后,则与“爱”字相对的字是“校”.



 如图,二次函数y=ax2-4ax与x轴交于O,A两点,y轴上有一点B(0,2),作经过O,A,B三点的⊙C,点P是第一象限内⊙C上的任意一点,连接BP,AP,当四边形OAPB面积最大时,点P的坐标为(3,3).
如图,二次函数y=ax2-4ax与x轴交于O,A两点,y轴上有一点B(0,2),作经过O,A,B三点的⊙C,点P是第一象限内⊙C上的任意一点,连接BP,AP,当四边形OAPB面积最大时,点P的坐标为(3,3).