题目内容
如图,在四边形ABCD中,∠BAC=∠ACD,∠B=∠D.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=3cm,BC=5cm,∠B=90°;点P从B点出发,以4cm/s的速度沿BA→AD→DC运动,点Q从B点出发,以1cm/s的速度沿BC方向运动,当一个点先到达点C时另一点就停止运动.问从运动开始经过多少时间,△BPQ的面积最大?
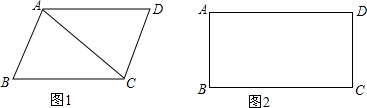
(1)求证:四边形ABCD是平行四边形;
(2)若AB=3cm,BC=5cm,∠B=90°;点P从B点出发,以4cm/s的速度沿BA→AD→DC运动,点Q从B点出发,以1cm/s的速度沿BC方向运动,当一个点先到达点C时另一点就停止运动.问从运动开始经过多少时间,△BPQ的面积最大?

考点:四边形综合题
专题:
分析:(1)先根据∠BAC=∠ACD,证明AB∥CD,然后证明△BAC≌△DCA得出AB=DC,最后根据对边平行且相等的四边形是平行四边形即可证得;
(2)分三种情况讨论求得.
(2)分三种情况讨论求得.
解答:(1)证明:∵∠BAC=∠ACD,
∴AB∥CD,
∵∠B=∠D,AC=CA,
∴△BAC≌△DCA,
∴AB=DC,
∴四边形ABCD是平行四边形;


(2)设从运动开始经过t秒时,△BPQ的面积为S,
当0≤t≤
时,如图2①,S=
BQ•PB=
×4t×t=2t2,S的最大值为
;
当
<t2时,如图2②,S=
(AP+BQ)•AB-
AP•AB=
(4t-3+t)×3-
(4t-3)×3=
t;S的最大值为3;
当2<t≤
时,如图2③,S=
BQ•PC=
t(11-4t)=-2t2+
t;无最大值;
所以S=
,
所以当从运动开始经过2秒时,△BPQ的面积最大的,其值为3cm2.
∴AB∥CD,
∵∠B=∠D,AC=CA,
∴△BAC≌△DCA,
∴AB=DC,
∴四边形ABCD是平行四边形;


(2)设从运动开始经过t秒时,△BPQ的面积为S,
当0≤t≤
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 8 |
当
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当2<t≤
| 11 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
所以S=
|
所以当从运动开始经过2秒时,△BPQ的面积最大的,其值为3cm2.
点评:此题考查了矩形的性质、平行四边形的判定、三角形的面积公式.能够借助函数的知识讨论图形的面积最值问题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
无论x取何有理数,代数式x2-2x+2的值一定是( )
| A、正数 | B、负数 |
| C、非正数 | D、非负数 |
 如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.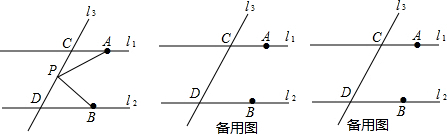
 一列快车从甲地匀速驶乙地,一列慢车从乙地匀速驶往甲地,慢车先发车半小时.设先发车辆行驶的时间为x/h,两车之间的距离为y/km,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
一列快车从甲地匀速驶乙地,一列慢车从乙地匀速驶往甲地,慢车先发车半小时.设先发车辆行驶的时间为x/h,两车之间的距离为y/km,图中的折线表示y与x之间的函数关系,根据图象解决以下问题: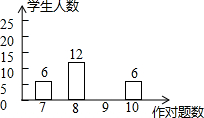 数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
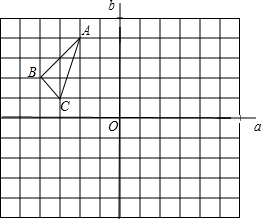 在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)
在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)