题目内容
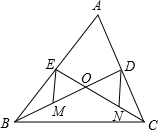 如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2
| 2 |
考点:平行四边形的判定与性质,三角形中位线定理
专题:
分析:(1)连接ED、MN,根据三角形中位线定理可得ED∥MN,ED=MN,进而得到四边形DEMN是平行四边形,再根据平行四边形的性质可得MD和NE互相平分;
(2)利用(1)中所求得出OC=2DN=4
,再利用勾股定理以及三角形面积公式求出S△OCB=
OB×CD即可.
(2)利用(1)中所求得出OC=2DN=4
| 2 |
| 1 |
| 2 |
解答:(1)证明:连接ED、MN,
∵CE、BD是△ABC的中线,
∴E、D是AB、AC中点,
∴ED∥BC,ED=
BC,
∵M、N分别为OB、OC的中点,
∴MN∥BC,MN=
BC,
∴ED∥MN,ED=MN,
∴四边形DEMN是平行四边形,
∴MD和NE互相平分;
(2)解:由(1)可得DN=EM=2
,
∵BD⊥AC,
∴∠ODC=90°,
∵N是OC的中点,
∴OC=2DN=4
(直角三角形斜边中线等于斜边的一半)
∵OD2+CD2=OC2=32,
(OD+CD)2=OD2+CD2+2OD×CD=72=49,
2OD×CD=49-32=17,
OD×CD=8.5,
∵OB=2OM=2OD,
∴S△OCB=
OB×CD=OD×CD=8.5.
∵CE、BD是△ABC的中线,
∴E、D是AB、AC中点,
∴ED∥BC,ED=
| 1 |
| 2 |
∵M、N分别为OB、OC的中点,
∴MN∥BC,MN=
| 1 |
| 2 |
∴ED∥MN,ED=MN,
∴四边形DEMN是平行四边形,
∴MD和NE互相平分;
(2)解:由(1)可得DN=EM=2
| 2 |

∵BD⊥AC,
∴∠ODC=90°,
∵N是OC的中点,
∴OC=2DN=4
| 2 |
∵OD2+CD2=OC2=32,
(OD+CD)2=OD2+CD2+2OD×CD=72=49,
2OD×CD=49-32=17,
OD×CD=8.5,
∵OB=2OM=2OD,
∴S△OCB=
| 1 |
| 2 |
点评:此题主要考查了平行四边形的判定与性质以及勾股定理和三角形面积求法等知识,得出OD×CD的值是解题关键.

练习册系列答案
相关题目
若关于x的不等式组
,其解集为-8<x<-4,则实数a的值为( )
|
| A、a<-4 | B、a=-4 |
| C、a>-8 | D、a=-8 |
一个等腰三角形两边长分别为5和6,则它的周长是( )
| A、11 | B、16 |
| C、17 | D、16或17 |
 如图,AC⊥CD于C,ED⊥CD于D,AB∥EF,∠CAE=25°,∠BAE=10°,则∠DEF=( )
如图,AC⊥CD于C,ED⊥CD于D,AB∥EF,∠CAE=25°,∠BAE=10°,则∠DEF=( )| A、30° | B、35° |
| C、40° | D、45° |
 如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数. 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥AC,交AC于P,连结MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标为(3,0),(3,4).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥AC,交AC于P,连结MP.已知动点运动了x秒.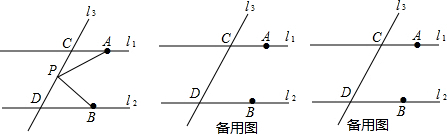
 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.