题目内容
20．
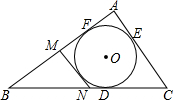如图，⊙O是△ABC的内切圆，D、E、F为切点，AB=18cm，BC=20cm，AC=12cm，MN切⊙O交AB于M，交BC于N，则△BNN的周长为（ ）| A． | 20cm | B． | 22cm | C． | 24cm | D． | 26cm |
分析 根据三角形内角和定理可得AE=AF，BD=BF，CE=CD，然后列方程求得BF的长，然后根据切线长定理可得△BMN的周长=BF+BD，据此即可求解．
解答 
解：设AF=xcm，BF=ycm，CD=zcm．
根据切线长定理可得：AE=AF=xcm，BD=BF=ycm，CE=CD=zcm．
根据题意得：$\left\{\begin{array}{l}{x+y=18}\\{y+z=20}\\{x+z=12}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=5}\\{y=13}\\{z=7}\end{array}\right.$，
则BF=BD=13cm．
又∵MG=MF，NG=ND，
∴△BMN的周长=BF+BD=26cm．
故选D．
点评 本题考查了切线长定理，正确理解△BMN的周长=BF+BD是解决本题的关键．
练习册系列答案
相关题目
在等边三角形ABC，DE∥AB，DE与边AB、AC分别交于D、E，△ADE是等边三角形吗？试说明理由．
如图，已知AC=6cm，BC=9cm，∠B=30°，∠D=115°，△ABC∽△DAC，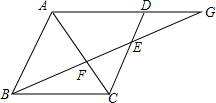
已知：如图，AC是?ABCD的对角线，G是AD延长线上的一点，BG交AC于F，交CD于E，求证：$\frac{BF}{FG}=\frac{FE}{BF}$．
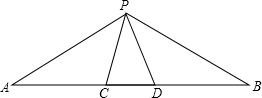如图，点C，D在线段AB上，P是直线AB外一点，连接PA，PB，PC，PD．已知△PCD是等边三角形，如果CD2=AC•DB，求∠APB的度数．