题目内容
8.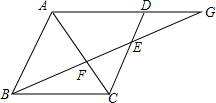 已知:如图,AC是?ABCD的对角线,G是AD延长线上的一点,BG交AC于F,交CD于E,求证:$\frac{BF}{FG}=\frac{FE}{BF}$.
已知:如图,AC是?ABCD的对角线,G是AD延长线上的一点,BG交AC于F,交CD于E,求证:$\frac{BF}{FG}=\frac{FE}{BF}$.
分析 由四边形ABCD是平行四边形,易证得△ABF∽△CEF,△AGF∽△CBF,然后由相似三角形的对应边成比例可得:BF:EF=AF:FC,AF:FC=FG:BF,继而证得结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△CEF,△AGF∽△CBF,
∴BF:EF=AF:FC,AF:FC=FG:BF,
∴BF:EF=FG:BF,
即$\frac{BF}{FG}=\frac{FE}{BF}$.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.两个负数相乘的结果为6,这两个数不可能为( )
| A. | -12和$\frac{1}{2}$ | B. | -2和-3 | C. | -1和-6 | D. | -1和-6或-2和-3 |
20.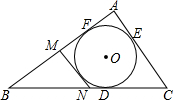 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
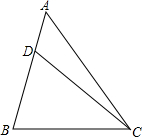 已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC.
已知D是△ABC的边AB上一点,AD:DB=1:2,∠A=45°,∠BDC=60°,求证:△CBD∽△ABC. 如图,直线EF表示一条铁路,A,B两点表示铁路的同侧的两个村庄,要在铁路EF旁建一车站C,使A,B两村到车站距离的和最短,请确定车站C的位置,并说明理由.
如图,直线EF表示一条铁路,A,B两点表示铁路的同侧的两个村庄,要在铁路EF旁建一车站C,使A,B两村到车站距离的和最短,请确定车站C的位置,并说明理由. 如图,△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,EF⊥BD于F.求证:CD:BD=DF:BF.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,EF⊥BD于F.求证:CD:BD=DF:BF.