题目内容
11. 如图,已知AC=6cm,BC=9cm,∠B=30°,∠D=115°,△ABC∽△DAC,
如图,已知AC=6cm,BC=9cm,∠B=30°,∠D=115°,△ABC∽△DAC,(1)求CD的长;
(2)求∠BAD的大小.
分析 (1)由△ABC∽△DAC,根据相似三角形的对应边成比例,即可求得CD的长;
(2)由△ABC∽△DAC,根据相似三角形的对应角相等,即可求得∠BAD的大小.
解答 解:(1)∵△ABC∽△DAC,
∴$\frac{AC}{BC}=\frac{CD}{AC}$,
∴$\frac{6}{9}=\frac{CD}{6}$,
解得:CD=4;
(2)∵△ABC∽△DAC,
∴∠BAC=∠D=115°,∠CAD=∠B=30°,
∴∠BAD=∠BAC+∠CAD=115°+30°=145°.
点评 此题考查了相似三角形的性质,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
6.在讨论方程$\frac{x}{x+3}$=$\frac{-3}{x+3}$的解的情况时,四位同学有下列四种不同的看法,你认为正确的是( )
| A. | 无解 | B. | 解为x=-3 | C. | 解为任意数 | D. | 不能确定 |
20.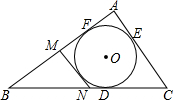 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
 如图,在△ABC中,DE∥BC,S△ADE=3,S△BCE=18,则S△BDE=6.
如图,在△ABC中,DE∥BC,S△ADE=3,S△BCE=18,则S△BDE=6. 如图,直线EF表示一条铁路,A,B两点表示铁路的同侧的两个村庄,要在铁路EF旁建一车站C,使A,B两村到车站距离的和最短,请确定车站C的位置,并说明理由.
如图,直线EF表示一条铁路,A,B两点表示铁路的同侧的两个村庄,要在铁路EF旁建一车站C,使A,B两村到车站距离的和最短,请确定车站C的位置,并说明理由.