题目内容
1.已知关于x,y的方程组$\left\{\begin{array}{l}{x-y=24}\\{3x+y=12m}\end{array}\right.$的解x,y满足0<x+y<6,则m的范围为2<m<3.分析 认真审题,首先将两个方程标上序号,再根据整体思想,用②式减去①式,即可求出x+y的值,进而即可得解.
解答 解:$\left\{\begin{array}{l}{x-y=24①}\\{3x+y=12m②}\end{array}\right.$,
②-①得:2x+2y=12m-24,
即:x+y=6m-12,
据题意,得:$\left\{\begin{array}{l}{6m-12>0}\\{6m-12<6}\end{array}\right.$,
解得:2<m<3.
故答案为:2<m<3.
点评 本题主要考查了二元一次方程组的解法,以及一元一次不等式组的解法,利用整体思想可以简化运算,是经常考查的题目,注意总计.

练习册系列答案
相关题目
6. 如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
 如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )| A. | 15粒 | B. | 18粒 | C. | 20粒 | D. | 31粒 |
11.一个布袋中有4个红球与6个白球,除颜色外完全相同,那么从布袋中随机摸一个球是白球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
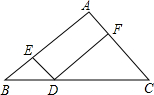 腰长为6的等腰直角△ABC中,D是BC上的一动点(不与BC重合),过点D作AB,
腰长为6的等腰直角△ABC中,D是BC上的一动点(不与BC重合),过点D作AB, 如图,有两条国道相交于点O,在∠AOB的内部有两村庄C、D,现要修建一加油站P,使点P到OA、OB的距离相等,且使PC=PD,用尺规作图,作出加油站P的位置(不写作法,保留作图痕迹).
如图,有两条国道相交于点O,在∠AOB的内部有两村庄C、D,现要修建一加油站P,使点P到OA、OB的距离相等,且使PC=PD,用尺规作图,作出加油站P的位置(不写作法,保留作图痕迹). 如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标(2,0),点C的坐标为(0,3)它的对称轴是直线x=-1.
如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标(2,0),点C的坐标为(0,3)它的对称轴是直线x=-1. 如图,A,B是反比例函数y=$\frac{6}{x}$(x>0)图象上的两点,AC⊥x轴于点C,BD⊥x轴于点D,求证:S△AOB=S梯形ABDC.
如图,A,B是反比例函数y=$\frac{6}{x}$(x>0)图象上的两点,AC⊥x轴于点C,BD⊥x轴于点D,求证:S△AOB=S梯形ABDC.