题目内容
1．
如图，已知l1∥l2，∠A=43°，∠1=60°，则∠2的度数为（ ）| A． | 103° | B． | 113° | C． | 120° | D． | 77° |
分析 根据平行线的性质求出∠ABC，根据三角形外角性质求出即可．
解答 解：∵l1∥l2，∠1=60°，
∴∠ABC=∠1=60°，
∵∠A=43°，
∴∠2=∠A+∠ABC=103°，
故选A．
点评 本题考查了平行线的性质，三角形的外角性质的应用，能根据平行线的性质求出∠ABC的度数是解此题的关键，注意：两直线平行，同位角相等．
练习册系列答案
阅读快车系列答案
相关题目
11．（x-3）（2x+1）=2x2+mx+n，则m，n的值分别是（ ）
| A． | 5，-3 | B． | -5，3 | C． | -5，-3 | D． | 5，3 |
12．下列二次根式中，是最简二次根式的是（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{12}$ | C． | $\sqrt{\frac{1}{2}}$ | D． | $\sqrt{{x}^{4}+{x}^{2}{y}^{2}}$ |
9．根据分式的基本性质，分式$\frac{-a}{a-2b}$可变形为（ ）
| A． | $\frac{a}{a+2b}$ | B． | $\frac{a}{-a-2b}$ | C． | $-\frac{a}{a+2b}$ | D． | $-\frac{a}{a-2b}$ |
16．某商城销售A、B两种电脑，其金价和售价如下表所示：
该商城计划购进两种电脑若干台，共需9.5万元，预计全部销售后可获毛利润共1.45万元【毛利润=（售价-进价）×销售量】
（1）该商城计划购进A、B两种电脑各多少台？
（2）通过市场调研，该商城决定在原计划的基础上减少A种电脑的购进数量，增加B种电脑的购进数量，已知B种电脑的增加数量是A种电脑减少数量的2倍，而且用于购进这两种电脑的总资金不超过10.3万元，该商场怎样进货，可使全部销售后的毛利润最大？并求出最大毛利润．
| A | B | |
| 进价（元/台） | 3000 | 2500 |
| 售价（元/台） | 3300 | 3000 |
（1）该商城计划购进A、B两种电脑各多少台？
（2）通过市场调研，该商城决定在原计划的基础上减少A种电脑的购进数量，增加B种电脑的购进数量，已知B种电脑的增加数量是A种电脑减少数量的2倍，而且用于购进这两种电脑的总资金不超过10.3万元，该商场怎样进货，可使全部销售后的毛利润最大？并求出最大毛利润．
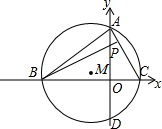如图，在平面直角坐标系中，A（0，6），P（0，4），点C为x轴正半轴上任一点，BP⊥AC交x轴于B点，△ABC内接于⊙M交y轴负半轴于D点．
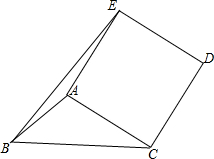如图，在△ABC中，∠ABC=45°，AB=$\sqrt{2}$，BC=4，以AC为边在AC的右侧作正方形ACDE，连接BE，求BE的长．
11．点A为数轴上表示-2的点，当点A沿数轴移动4个单位长时，它所表示的数是（ ）
| A． | 2 | B． | 2或-6 | C． | -6 | D． | 不同于以上答案 |