题目内容
13. 如图,在平面直角坐标系中,点C、D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点D作BA∥x轴交y轴于点A,BC∥y轴且交曲线于点C,已知BD=3AD,若四边形ODBC的面积为6,则k=2.
如图,在平面直角坐标系中,点C、D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点D作BA∥x轴交y轴于点A,BC∥y轴且交曲线于点C,已知BD=3AD,若四边形ODBC的面积为6,则k=2.
分析 延长BC交x轴于点E,连接OB,根据反比例函数系数k的几何意义得出S△AOD=S△EOC,再由矩形的性质得出S△AOB=S△EOB,故可得出△OBD的面积,再由BD=3AD可得出△AOD的面积,进而可得出k的值.
解答 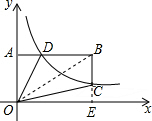 解:延长BC交x轴于点E,连接OB,
解:延长BC交x轴于点E,连接OB,
∵BA∥x轴,BC∥y轴,
∴S△AOD=S△EOC,四边形OABE是矩形,
∴S△AOB=S△EOB,
∴S△OBD=S△OBC=3,
∵BD=3AD,
∴S△AOD=$\frac{1}{3}$S△OBD=1,
∴k=2S△AOD=2.
故答案为:2.
点评 本题考查的是反比例函数图象上点的坐标特点,根据题意作出辅助线,利用矩形的性质求解是解答此题的关键.

练习册系列答案
相关题目
8. 如图,在?ABCD中,AE平分∠BAD,己知∠AEB=63°,则∠D的度数为( )
如图,在?ABCD中,AE平分∠BAD,己知∠AEB=63°,则∠D的度数为( )
 如图,在?ABCD中,AE平分∠BAD,己知∠AEB=63°,则∠D的度数为( )
如图,在?ABCD中,AE平分∠BAD,己知∠AEB=63°,则∠D的度数为( )| A. | 63° | B. | 72° | C. | 54° | D. | 60° |
5.计算(-2a2b)(3a3b2)的结果是( )
| A. | -6a5b3 | B. | -6a3b5 | C. | 6a5b3 | D. | 6a3b5 |
3.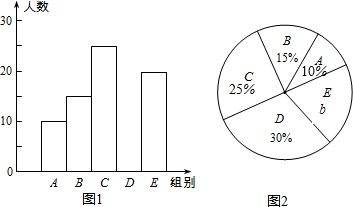 某中学举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
某中学举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
(1)在统计表中,a=30,b=20%.
(2)补全条形统计图,计算扇形统计图中“D组”所对应的圆心角的度数;
(3)若该校共有500名学生,如果听写正确的字数少于16个定为不合格,请你估计这所中学本次比赛听写不合格的学生人数.
 某中学举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
某中学举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:(1)在统计表中,a=30,b=20%.
(2)补全条形统计图,计算扇形统计图中“D组”所对应的圆心角的度数;
(3)若该校共有500名学生,如果听写正确的字数少于16个定为不合格,请你估计这所中学本次比赛听写不合格的学生人数.
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | a |
| E | 32≤x<40 | 20 |
 如图,直线l与直线a,b相交,且a∥b,∠1=45°,则∠2的度数是45°.
如图,直线l与直线a,b相交,且a∥b,∠1=45°,则∠2的度数是45°.