题目内容
6.已知x为任意实数,给出下列关于x的不等式:①x2+1≥2x;②x2+1≥-3x;③$\frac{x}{{x}^{2}+1}$≥-$\frac{1}{2}$;④$\frac{{x}^{2}+x+1}{{x}^{2}+1}$$≤\frac{3}{2}$.
其中一定成立的是①③④(选出所有成立的不等式的序号)
分析 ①根据不等式(x-1)2≥0进行变形;②将x=-1代入原不等式进行判断;③根据不等式x2+2x+1≥0进行变形,得到x2+1≥-2x,再根据2(x2+1)>0进行变形即可;④在不等式x2+1≥2x的两边都除以2(x2+1),进行变形即可.
解答 解:①∵x为任意实数,
∴(x-1)2≥0,即x2-2x+1≥0
∴x2+1≥2x,故①成立;
②∵x为任意实数,
∴当x=-1时,②不成立;
③∵x为任意实数,
∴x2+2x+1≥0,即x2+1≥-2x,
∵x为任意实数,
∴2(x2+1)>0,
将x2+1≥-2x两边都除以2(x2+1),得
$\frac{1}{2}$≥-$\frac{x}{{x}^{2}+1}$,即$\frac{x}{{x}^{2}+1}$≥-$\frac{1}{2}$,故③成立;
④∵x2+1≥2x,
∴两边都除以2(x2+1),得
$\frac{x}{{x}^{2}+1}$≤$\frac{1}{2}$,
∴$\frac{x}{{x}^{2}+1}$+1≤$\frac{1}{2}$+1,
即$\frac{{x}^{2}+x+1}{{x}^{2}+1}$$≤\frac{3}{2}$,故④成立.
故答案为:①③④
点评 本题主要考查了不等式的基本性质,解决问题的关键是运用x2-2x+1≥0和x2+2x+1≥0等结论.应用不等式的性质应注意:在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
6.据2016年南平市政府工作报告,2015年全市外贸出口11.26亿美元,这一数据用科学记数法表示为( )
| A. | 0.1126×1010 | B. | 1.126×109 | C. | 1.126×108 | D. | 11.26×107 |
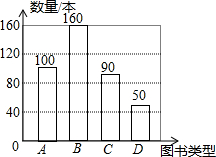 王洋同学调查了光明中学图书馆中某周A,B,C,D四类图书的借阅人数(每人每次只能借阅一本图书),并绘制成了如图所示的条形统计图,若根据该条形统计图绘制扇形统计图,则B类图书借阅人数所在的扇形的圆心角的度数为144°.
王洋同学调查了光明中学图书馆中某周A,B,C,D四类图书的借阅人数(每人每次只能借阅一本图书),并绘制成了如图所示的条形统计图,若根据该条形统计图绘制扇形统计图,则B类图书借阅人数所在的扇形的圆心角的度数为144°.