题目内容
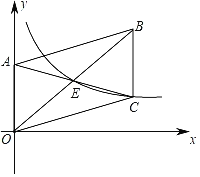
【题目】已知抛物线![]() ,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
(Ⅰ)求点A,B和点C的坐标;
(Ⅱ)已知P是线段![]() 上的一个动点.
上的一个动点.
①若![]() 轴,交抛物线于点Q,当
轴,交抛物线于点Q,当![]() 取最大值时,求点P的坐标;
取最大值时,求点P的坐标;
②求![]() 的最小值.
的最小值.
【答案】(Ⅰ)A![]() ,B
,B![]() ,C
,C![]() ;(Ⅱ)①
;(Ⅱ)① ;②
;②![]()
【解析】
(Ⅰ)令![]() ,代入抛物线解析式即可求出A、B的坐标,令
,代入抛物线解析式即可求出A、B的坐标,令![]() 从而得出C点坐标;
从而得出C点坐标;
(Ⅱ)①设![]() 代入B、C坐标即可得出直线解析式,设
代入B、C坐标即可得出直线解析式,设![]() ,
,![]() ,则
,则![]() ,且Q在P上方,分别表示出PQ,BP即可得出PQ+BP的表达式,对表达式进行配方即可得出结果,②如图,延长
,且Q在P上方,分别表示出PQ,BP即可得出PQ+BP的表达式,对表达式进行配方即可得出结果,②如图,延长![]() 至点D,使得
至点D,使得![]() ,连接
,连接![]() ,作
,作![]() 轴于点E,过点P作
轴于点E,过点P作![]() 于点H,可证的
于点H,可证的![]() 是等腰直角三角形,由垂线段最短可知,当
是等腰直角三角形,由垂线段最短可知,当![]() ,
,![]() ,
,![]() 共线时
共线时![]() 取得最小值,根据题目已知条件得出D点坐标,表示出
取得最小值,根据题目已知条件得出D点坐标,表示出![]() 即可得出结果.
即可得出结果.
解:(Ⅰ)令![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() .
.
∴A点坐标为![]() ,B点坐标为
,B点坐标为![]() .
.
令![]() ,则
,则![]() .
.
∴C点坐标为![]() .
.
(Ⅱ)①设:![]() ,将
,将![]() ,
,![]() 分别代入得,
分别代入得,
![]() ,解得
,解得 ,故
,故![]() .
.
可设![]() ,
,![]() ,则
,则![]() ,且Q在P上方.
,且Q在P上方.
所以![]() .
.
又 .
.
故 .
.
当![]() 时取得最大值,此时
时取得最大值,此时 .
.

②如图,延长![]() 至点D,使得
至点D,使得![]() ,连接
,连接![]() ,作
,作![]() 轴于点E,过点P作
轴于点E,过点P作![]() 于点H.
于点H.
由![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
则![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
![]() ,由垂线段最短可知,当
,由垂线段最短可知,当![]() ,
,![]() ,
,![]() 共线时
共线时![]() 取得最小值.
取得最小值.
∵![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
可得点D的坐标为![]() .
.
∴![]() ,
,
![]() ,代入可得
,代入可得![]() ,
,
解得![]() ,故有
,故有![]() .
.
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目