题目内容
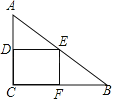
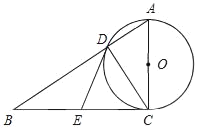
【题目】已知:![]() 中,
中,![]() 是直径,弦
是直径,弦![]() .
.
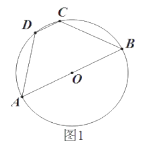
![]() 如图1,求证:
如图1,求证:![]()
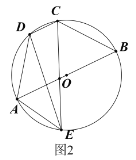
![]() 如图2,点
如图2,点![]() 在圆上,连接
在圆上,连接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
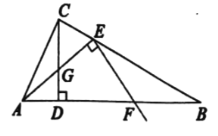
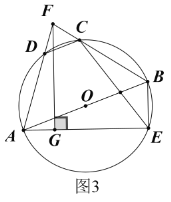
![]() 如图3,在
如图3,在![]() 的条件下,分别延长线段
的条件下,分别延长线段![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】![]() 详见解析;
详见解析; ![]() ;
; ![]()
【解析】
(1)连接OC,OD,证明△AOD≌△BOC即可;
(2)作直径DQ,连接CQ,则∠DCQ=90°,根据DC∥AB,可得∠CHB=∠DCQ=90°,根据弧DC=弧DC,可得tan∠Q=tan∠DEC=![]() ,可设DC=7k,则CQ=24k,根据已知可得出CH=
,可设DC=7k,则CQ=24k,根据已知可得出CH=![]() CQ=12k,HB=9k,即可得出tan∠B,根据弧AC=弧AC,可得∠CEA=∠B,即可得出答案;
CQ=12k,HB=9k,即可得出tan∠B,根据弧AC=弧AC,可得∠CEA=∠B,即可得出答案;
(3)由现有条件可得AF=BF,连接FO,得∠OFG=∠EAB=α,再设∠AFG=β,在AE上取GN=AG=3,连接FN,则FN=FA=FB,推出tan∠NBE=![]() ,设BE=3n,则NE=4n,GE=2BE=6n,可推出AB=
,设BE=3n,则NE=4n,GE=2BE=6n,可推出AB=![]() =
=![]() ,所以在Rt△FOB中,tan∠OBF=
,所以在Rt△FOB中,tan∠OBF=![]() ,设FO=4t,OB=3t,即可得出FB,根据FA=FB即可确定答案.
,设FO=4t,OB=3t,即可得出FB,根据FA=FB即可确定答案.
(1)如图,连接OC,OD,

∵OC=OD,
∴∠ODC=∠OCD,
∵DC∥AB,
∴∠AOD=∠ODC=∠OCD=∠BOC,
又∵OA=OB,
∴△AOD≌△BOC,
∴AD=BC;
(2)作直径DQ,连接CQ,则∠DCQ=90°,
∵DC∥AB,
∴∠CHB=∠DCQ=90°,
又∵AB是直径,
∴CH=QH=![]() CQ,
CQ,
∴OH是△DCQ的中位线,
∴OH=![]() DC,
DC,
∵弧DC=弧DC,
∴∠DEC=∠Q,
∴tan∠Q=tan∠DEC=![]() ,
,
设DC=7k,则CQ=24k,
∴CH=![]() CQ=12k,OH=
CQ=12k,OH=![]() DC=
DC=![]() k,
k,
2r=DQ=![]() =25k,
=25k,
∴OB=r=![]() k,
k,
∴HB=OB-OH=![]() k-
k-![]() k=9k,
k=9k,
∴tan∠B=![]() =
=![]() =
=![]() ,
,
∵弧AC=弧AC,
∴∠CEA=∠B,
∴tan∠CEA= tan∠B=![]() ;
;
(3)如图1,
∵∠AOD =∠BOC,
∴∠AOD+∠DOC=∠BOC+∠DOC,即∠AOC=∠BOD,
∴弧AC=弧BD,
∴∠FAB=∠FBA,
∴AF=BF,
如图3,连接FO,
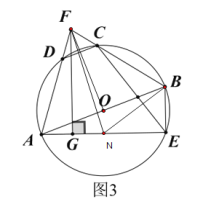
∵AO=BO,
∴∠BFO=∠AFO,FO⊥AB,
又∵FG⊥AE,
∴∠FOA=∠AGF=90°,
∴∠OFG=∠EAB=α,
设∠AFG=β,
则∠BFO=∠AFO=∠OFG+∠AFG=α+β,
∴∠AFB=2(α+β),
在AE上取GN=AG=3,连接FN,则FN=FA=FB,
∴∠GFN=∠AFG=β,
∴∠NFB=∠AFB-∠AFN=2(α+β)-2β=2α,
∴∠FBN=∠FNB=![]() =90°-α,
=90°-α,
∵AB是直径,
∴∠AEB=90°,
∴∠ABE=90°-∠EAB=90°-α=∠FBN,
∴∠ABE-∠ABN=∠FBN-∠ABN,
∴∠NBE=∠ABC,
∴tan∠NBE=![]() ,
,
∴设BE=3n,则NE=4n,
GE=2BE=6n,
∴6n=3+4n,
∴n=![]() ,
,
∴BE=![]() ,AE=12,
,AE=12,
∴AB=![]() =
=![]() ,
,
在Rt△FOB中,tan∠OBF=![]() ,
,
∴设FO=4t,OB=3t,
∴FB=![]() =5t,
=5t,
∴FB=![]() OB=
OB=![]() ×
×![]() =
=![]() ,
,
∴FA=FB=![]() .
.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】如下表,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中仼意三个相邻格子中所填整数之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019个格子中的数为______;
(3)前2020个格子中所填整数之和为______.
(4)前![]() 个格子中所填整数之和是否可能为2020?若能,求出
个格子中所填整数之和是否可能为2020?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.