题目内容
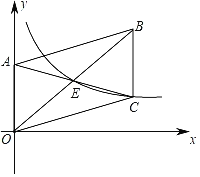
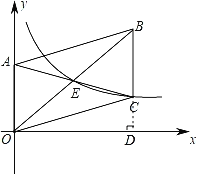
【题目】如图，已知平面直角坐标系中A点坐标为（0，4），以OA为一边在第一象限作平行四边形OABC，对角线AC、OB相交于点E，AB＝2OA．若反比例函数y＝
的图象恰好经过点C和点E，则k的值为______．
【答案】
【解析】
过点C作CD⊥x轴于点D，由已知条件及平行四边形的性质可得BC＝OA＝4，OC＝AB＝8，设C（x，
），则点E（
，
），点B（x，+4），分别按照点E在反比例函数图象上和作为线段BD的中点，用两种方式表示出点E的纵坐标，从而得到关于x和k的等式，解得x和k的关系，再在Rt△COD中，由勾股定理得关于k的方程，解得k的值，舍去负值，即可得出答案．
解：如图，过点C作CD⊥x轴于点D，
∵A点坐标为（0，4），AB＝2OA．
∴OA＝4，AB＝8，
∵四边形OABC为平行四边形，
∴BC＝OA＝4，OC＝AB＝8，点B、C、D共线，
∵反比例函数y＝的图象恰好经过点C和点E，
∴设C（x，），则点E（，），点B（x，+4），
∵E为平行四边形对角线的交点，
∴E为OB中点，
∴点E的坐标又可以表示为：（，
+2），
∴＝+2，
解得：＝
，
∴x＝
，
∴在Rt△COD中，由勾股定理得：
+
＝64，
解得k＝．（负值舍去，因为反比例函数图象位于第一象限）．
故答案为：．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】如下表，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中仼意三个相邻格子中所填整数之和都相等．
|
|
|
| 5 | 4 | …… |
（1）可求得
_____；
_____；
_____．
（2）第2019个格子中的数为______；
（3）前2020个格子中所填整数之和为______．
（4）前
个格子中所填整数之和是否可能为2020？若能，求出的值，若不能，请说明理由．
