题目内容
6. 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度,你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度,你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
分析 延长PQ交直线AB于点E,设测出AB的长度为m米,在直角△APE和直角△BPE中,根据三角函数利用PE表示出AE和BE,根据AB=AE-BE即可列出方程求得PE的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
解答 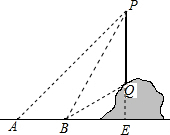 解:同意他们的测量方案;
解:同意他们的测量方案;
延长PQ交直线AB于点E,
设测出AB的长度为m米.
在直角△APE中,∠A=45°,
则AE=PE;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=$\frac{\sqrt{3}}{3}$PE,
∵AB=AE-BE=m,
则PE-$\frac{\sqrt{3}}{3}$PE=m,
解得:PE=$\frac{3+\sqrt{3}}{2}$m.
则BE=$\frac{3+\sqrt{3}}{2}$m-m=$\frac{1+\sqrt{3}}{2}$m.
在直角△BEQ中,QE=$\frac{\sqrt{3}}{3}$BE=$\frac{\sqrt{3}}{3}$($\frac{1+\sqrt{3}}{2}$m)=$\frac{\sqrt{3}+3}{6}$m.
∴PQ=PE-QE=$\frac{3+\sqrt{3}}{2}$m-$\frac{\sqrt{3}+3}{6}$m=$\frac{\sqrt{3}+3}{3}$m.
点评 本题考查解直角三角形的应用,注意掌握当两个直角三角形有公共边时,先求出这条公共边的长是解答此类题的一般思路.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.-|3.14-π|的值是( )
| A. | 3.14+π | B. | 3.14-π | C. | π-3.14 | D. | 0 |
14.已知a2+bc=14,b2-2bc=-6,则3a2+4b2-5bc的值是( )
| A. | 8 | B. | 12 | C. | 16 | D. | 18 |
6.若xm=2,xn=3,则x2m+3n等于( )
| A. | 6 | B. | 13 | C. | 36 | D. | 108 |
 如图所示,点A在线段CB上,AC=$\frac{1}{2}AB$,点D是线段BC的中点.若CD=3,求线段AD的长.
如图所示,点A在线段CB上,AC=$\frac{1}{2}AB$,点D是线段BC的中点.若CD=3,求线段AD的长. 如图,按此规律,第6行最后一个数字是16,则第36行最后一个数是106.
如图,按此规律,第6行最后一个数字是16,则第36行最后一个数是106.