题目内容
11.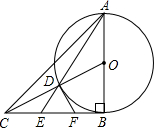 如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.
如图,在△ABC中,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.(1)求证:△CDF∽△CBO;
(2)若ED•EA=8,求BE和CE的长.
分析 (1)根据切线的性质得到DF⊥OD,根据相似三角形的判定定理即可得到结论;
(2)连接BD,由AB为直径,得到BD⊥AE,根据相似三角形的想知道的BE2=AE•DE=8,得到BE=2$\sqrt{2}$,根据切线的性质得到FB=DF,得到EF=BF=DF=$\frac{1}{2}$BE=$\sqrt{2}$,根据相似三角形的性质即可得到结论.
解答 (1)证明:∵DF是⊙O的切线,
∴DF⊥OD,
∴∠CDF=∠CBO=90°,
∵∠DCF=∠OCB,
∴△CDF∽△CBO;
(2)连接BD,
∵AB为直径,
∴BD⊥AE,
∴∠BDE=∠ABE,
∴△ABE∽△BDE,
∴$\frac{BE}{AE}$=$\frac{DE}{BE}$,
∴BE2=AE•DE=8,
∴BE=2$\sqrt{2}$,
∵FD是⊙O的切线,
∵∠ABC=90°,
∴CB是⊙O的切线,
∴FB=DF,
∵∠BDE=90°,
∴EF=BF=DF=$\frac{1}{2}$BE=$\sqrt{2}$,
∵△CDF∽△CBO,
∴$\frac{DF}{BO}$=$\frac{CD}{BC}$,
∴$\frac{DF}{CD}$=$\frac{BO}{CB}$,
∵AB=BC,
∴$\frac{DF}{CD}$=$\frac{BO}{CB}$=$\frac{1}{2}$,
∴DF=$\frac{1}{2}$CD,
∴CD=2$\sqrt{2}$,
∴CF=$\sqrt{10}$,
∴CE=$\sqrt{10}$-$\sqrt{2}$.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,切线的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
1.化简(x3)2的结果是( )
| A. | 2x3 | B. | x5 | C. | x6 | D. | x9 |
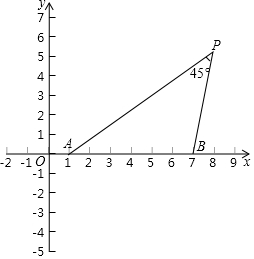 如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).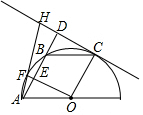 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.