Question

4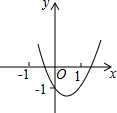．二次函数y=ax²+bx+c（a≠0）的图象如图所示，则下列关系式中正确的是（　　）

• A． ac＞0
• B． b+2a＜0
• C． b²-4ac＞0
• D． a-b+c＜0

Answer 1

分析 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

解答 解：A、由函数图象可知二次函数y=ax²+bx+c的开口向上，即a＞0，交于y轴的负半轴c＜0，ac＜0，故本选项错误；
B、由函数图象可知对称轴x=-$\frac{b}{2a}$＜1，所以-b＜2a，即2a+b＞0，故本选项错误；
C、由函数图象可知二次函数y=ax²+bx+c与x轴有两个交点，则b²-4ac＞0．故本选项正确；
D、由函数图象可知当x=-1时，y＞0，a-b+c＞0，故本选项错误．
故选C．

点评 考查二次函数图象与系数的关系；用到的知识点为：二次函数的开口向上，a＞0；二次函数与y轴交于负半轴，c＜0；二次函数与x轴有2个交点，b²-4ac＞0；a-b+c的符号用当x=-1时，函数值的正负判断．