题目内容
9.甲、乙两地相距480千米,一辆慢车从甲地开往乙地,一辆快车从乙地开往甲地,两车同时出发,经过3小时相遇,相遇时快车比慢车多行了120千米.(1)求慢车和快车的速度;
(2)甲、乙两地间有A、B两个加油站,相距160千米,若快车进入B加油站时,慢车恰好进入A加油站,求加油站B离甲地的距离.
分析 (1)由题意可知:快车比慢车每小时多行120÷3=40千米,设慢车速度为x千米/小时,则快车速度为(x+40)千米/小时,根据两车行的路程和为480千米列方程解答即可;
(2)设快车进入B加油站的时间为a小时,根据两车行的路程和为480-160=320或480+160=640千米列方程解答,进一步求得答案即可.
解答 解:(1)设慢车速度为x千米/小时,则快车速度为(x+120÷3)千米/小时,由题意得
3x+3(x+120÷3)=480
解得:x=60
x+120÷3=100
答:慢车速度为60千米/小时,快车速度为100千米/小时;
(2)设快车进入B加油站的时间为a小时,由题意得
60a+100a=480-160或60a+100a=480+160
解得:a=2或4
60×2+160=280(千米)或60×4-160=80(千米)
答:加油站B离甲地的距离为280或80千米.
点评 此题考查一元一次方程的实际运用,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.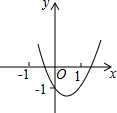 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )
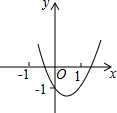 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式中正确的是( )| A. | ac>0 | B. | b+2a<0 | C. | b2-4ac>0 | D. | a-b+c<0 |
 如图,在平面直角坐标系中,已知点A(0,4),B(-3,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为(0,$\frac{3}{2}$).
如图,在平面直角坐标系中,已知点A(0,4),B(-3,0),连接AB.将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则点C的坐标为(0,$\frac{3}{2}$). 如图,正方形OABC,ADEF的顶点A、D、C在坐标轴上,点F在AB 上,点B、E在函数$y=\frac{4}{x}$(x>0)的图象上,若阴影部分的面积为12-$4\sqrt{5}$,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1).
如图,正方形OABC,ADEF的顶点A、D、C在坐标轴上,点F在AB 上,点B、E在函数$y=\frac{4}{x}$(x>0)的图象上,若阴影部分的面积为12-$4\sqrt{5}$,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1). 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧. 已知:如图,点O为AC、BD的交点,且AB=DC,∠A=∠D,求证:∠OBC=∠OCB.
已知:如图,点O为AC、BD的交点,且AB=DC,∠A=∠D,求证:∠OBC=∠OCB.