Question

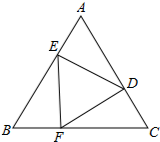如图，D、E、F分别是等边△ABC三边上的点，AE=BF=CD．求证：△ABC∽△DEF．

Answer 1

考点：相似三角形的判定

专题：证明题

分析：首先证明三角形DEF是等边三角形，所以可得∠EFD=∠A=∠B=∠FDE=60°，所以△ABC∽△DEF．

解答：证明：∵△ABC是等边三角形，
∴AB=BC=AC，
∵AE=BF=CD，
∴EB=FC=DA，
∵∠A=∠B=∠C=60°，
∴△AED≌△BEF≌△CFD，
∴ED=EF=FD，
∴△EFD是等边三角形，
∴∠EFD=∠A=∠B=∠FDE=60°，
∴△ABC∽△EFD．

点评：本题考查了相似三角形的判定和性质、等边三角形的性质、全等三角形的判定和性质，题目的综合性较强，难度中等．