题目内容
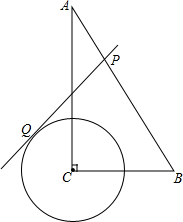 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为考点:切线的性质
专题:
分析:当PC⊥AB时,线段PQ最短;连接CP、CQ,根据勾股定理知PQ2=CP2-CQ2,先求出CP的长,然后由勾股定理即可求得答案.
解答:解:连接CP、CQ;如图所示: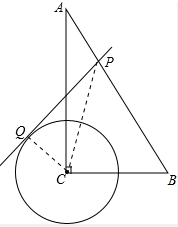
∵PQ是⊙C的切线,
∴CQ⊥PQ,∠CQP=90°,
根据勾股定理得:PQ2=CP2-CQ2,
∴当PC⊥AB时,线段PQ最短,
∵在Rt△ACB中,∠A=30°,BC=2,∴AB=2BC=4,AC=2
,
∴CP=
=
=
,
∴PQ=
=
=
,
∴PQ的最小值是
;
故答案为:
.

∵PQ是⊙C的切线,
∴CQ⊥PQ,∠CQP=90°,
根据勾股定理得:PQ2=CP2-CQ2,
∴当PC⊥AB时,线段PQ最短,
∵在Rt△ACB中,∠A=30°,BC=2,∴AB=2BC=4,AC=2
| 3 |
∴CP=
| AC•BC |
| AB |
2
| ||
| 4 |
| 3 |
∴PQ=
| CP2-CQ2 |
| 3-1 |
| 2 |
∴PQ的最小值是
| 2 |
故答案为:
| 2 |
点评:本题考查了切线的性质以及勾股定理的运用;注意掌握辅助线的作法,注意当PC⊥AB时,线段PQ最短是关键.

练习册系列答案
相关题目
 如图,线段AD=16cm,线段AC=BD=10cm,E、F分别是线段AB、CD的中点,则线段EF的长为
如图,线段AD=16cm,线段AC=BD=10cm,E、F分别是线段AB、CD的中点,则线段EF的长为 已知抛物线y1=x2+2(m+2)x+m-2与x轴交于A,B两点(点A在点B左侧),对称轴为直线x=-1.
已知抛物线y1=x2+2(m+2)x+m-2与x轴交于A,B两点(点A在点B左侧),对称轴为直线x=-1.
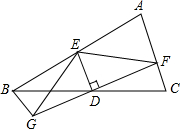 如图,△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF,交AB于点E连接EG、EF.
如图,△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF,交AB于点E连接EG、EF.