题目内容
 已知抛物线y1=x2+2(m+2)x+m-2与x轴交于A,B两点(点A在点B左侧),对称轴为直线x=-1.
已知抛物线y1=x2+2(m+2)x+m-2与x轴交于A,B两点(点A在点B左侧),对称轴为直线x=-1.(1)m的值为
| x | … | … | |||||
| y | … | … |
考点:二次函数的图象,二次函数与不等式(组)
专题:
分析:(1)根据对称轴列出方程求解即可得到m的值,然后根据二次函数图象的画法描点,连接即可;
(2)根据函数图象写出抛物线在直线上方部分的x的取值范围即可.
(2)根据函数图象写出抛物线在直线上方部分的x的取值范围即可.
解答:解:(1)抛物线对称轴为直线x=-
=-1,
解得m=-1,
函数解析式为y=x2+2x-3,

(2)∵直线y2=kx+b过点B且与抛物线交于点P(-2,-3),
∴x<-2或x>1时,y2≤y1.
| 2(m+2) |
| 2 |
解得m=-1,
函数解析式为y=x2+2x-3,
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | 0 | -3 | -4 | -3 | 0 | … |

(2)∵直线y2=kx+b过点B且与抛物线交于点P(-2,-3),
∴x<-2或x>1时,y2≤y1.
点评:本题考查了二次函数图象,二次函数与不等式,熟练掌握二次函数的对称轴的求法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、带根号的数都是无理数 |
| B、无限小数都是无理数 |
| C、两个无理数之和一定是无理数 |
| D、两个无理数之积不一定是无理数 |
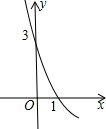 如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )
如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )| A、-3<s<3 | B、s>0 |
| C、s>3 | D、0<s<3 |
 如图,线段AD=18cm,线段AC=BD=12cm,E、F分别是线段AB、CD的中点,求线段EF的长.
如图,线段AD=18cm,线段AC=BD=12cm,E、F分别是线段AB、CD的中点,求线段EF的长.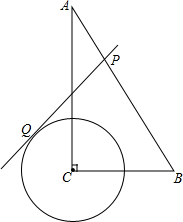 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为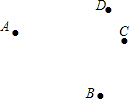 如图,已知平面上有四个点A,B,C,D四个村庄.
如图,已知平面上有四个点A,B,C,D四个村庄.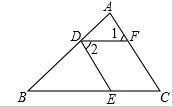 如图所示,点D,E,F分别在AB,BC,AC上.
如图所示,点D,E,F分别在AB,BC,AC上.