题目内容
 如图,线段AD=16cm,线段AC=BD=10cm,E、F分别是线段AB、CD的中点,则线段EF的长为
如图,线段AD=16cm,线段AC=BD=10cm,E、F分别是线段AB、CD的中点,则线段EF的长为考点:两点间的距离
专题:
分析:根据线段的和差,可得BC的长,可得(AB+CD)的长,根据线段中点的性质AE、FD的长,再根据线段的和差,可得(AE+FD),可得EF的长.
解答:解:由线段的和差,得
AC+BD=AC+(CD+BC)=AC+CD+BC=10+10=20cm.
由线段的和差,得
AC+CD=AD=16cm,
16+BC=20,
解得BC=4cm,
再由线段和差,得AB+CD=AD-BC=16-4=12cm.
由E、F分别是线段AB、CD的中点,得
AE=
AB,FD=
CD.
由等式的性质,得AE+FD=
AB+
CD=
(AB+CD)=
×12=6cm.
由线段的和差,得
EF=AD-(AE+FD)=16-6=10cm,
故答案为:10cm.
AC+BD=AC+(CD+BC)=AC+CD+BC=10+10=20cm.
由线段的和差,得
AC+CD=AD=16cm,
16+BC=20,
解得BC=4cm,
再由线段和差,得AB+CD=AD-BC=16-4=12cm.
由E、F分别是线段AB、CD的中点,得
AE=
| 1 |
| 2 |
| 1 |
| 2 |
由等式的性质,得AE+FD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差,得
EF=AD-(AE+FD)=16-6=10cm,
故答案为:10cm.
点评:本题考查了两点间的距离,利用线段的和差得出(AB+CD)、(AE+FD)的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一件衣服原价100元,连续两次降价后卖81元,则平均每次降价的百分数是( )
| A、9% | B、10% |
| C、9.5% | D、8.5% |
下列说法正确的是( )
| A、带根号的数都是无理数 |
| B、无限小数都是无理数 |
| C、两个无理数之和一定是无理数 |
| D、两个无理数之积不一定是无理数 |
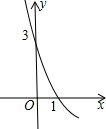 如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )
如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )| A、-3<s<3 | B、s>0 |
| C、s>3 | D、0<s<3 |
 如图,线段AD=18cm,线段AC=BD=12cm,E、F分别是线段AB、CD的中点,求线段EF的长.
如图,线段AD=18cm,线段AC=BD=12cm,E、F分别是线段AB、CD的中点,求线段EF的长.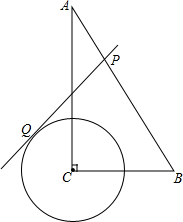 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为