题目内容
已知抛物线y=-x2+bx+c的对称轴是直线x=-1,且经过点(2,-3),求这个二次函数的表达式.
考点:待定系数法求二次函数解析式
专题:
分析:由抛物线的一般形式可知:a=-1,由对称轴方程x=-
,可得一个等式-
=-1①,然后将点(2,-3)代入y=-x2+bx+c即可得到等式-4+2b+c=-3②,然后将①②联立方程组解答即可.
| b |
| 2a |
| b |
| 2×(-1) |
解答:解:根据题意,得:
,
解得
,
所求函数表达式为y=-x2-2x+5.
|
解得
|
所求函数表达式为y=-x2-2x+5.
点评:此题考查了用待定系数法求二次函数的解析式,解题的关键是:熟练掌握待定系数法及对称轴表达式x=-
.
| b |
| 2a |

练习册系列答案
相关题目
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )
| A、4tan50° |
| B、4tan40° |
| C、4sin50° |
| D、4sin40° |
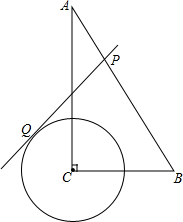 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为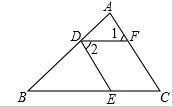 如图所示,点D,E,F分别在AB,BC,AC上.
如图所示,点D,E,F分别在AB,BC,AC上. 如图,图①所示的正方体木块,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,分别画出②从正面看、从左面看和从上面看到的平面图形.
如图,图①所示的正方体木块,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,分别画出②从正面看、从左面看和从上面看到的平面图形.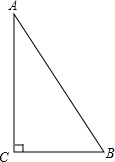 已知,在△ABC中,∠C=90°,sinA=
已知,在△ABC中,∠C=90°,sinA=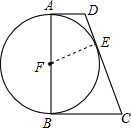 如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.
如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.