题目内容
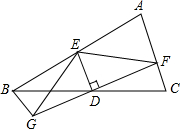 如图,△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF,交AB于点E连接EG、EF.
如图,△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF,交AB于点E连接EG、EF.(1)求证:BG=CF;
(2)当∠A=90°时,判断BE、CF、EF之间存在的等量关系,并说明理由.
考点:全等三角形的判定与性质,线段垂直平分线的性质,勾股定理
专题:
分析:(1)由BG∥AC得出∠DBG=∠DCF,从而根据ASA证得△BGD≌△CFD,即可证得结论.
(2)根据△BGD≌△CFD得出GD=FD,BG=CF,然后根据线段的垂直平分线的性质求得EG=EF,根据平行线的性质证得∠EBG=90°,最后根据勾股定理即可求得BE2+BG2=EG2,通过等量代换即可得到BE、CF、EF之间存在的等量关系.
(2)根据△BGD≌△CFD得出GD=FD,BG=CF,然后根据线段的垂直平分线的性质求得EG=EF,根据平行线的性质证得∠EBG=90°,最后根据勾股定理即可求得BE2+BG2=EG2,通过等量代换即可得到BE、CF、EF之间存在的等量关系.
解答:解:(1)∵BG∥AC,
∴∠DBG=∠DCF,
∵D是BC的中点,
∴BD=CD,
在△BGD和△CFD中,
,
∴△BGD≌△CFD(ASA),
∴BG=CF.
(2)BE2+CF2=EF2;
∵△BGD≌△CFD,
∴GD=FD,BG=CF,
又∵DE⊥FG,
∴EG=EF(垂直平分线上的点到线段两端点的距离相等),
∵∠A=90°,AC∥BG,
∴∠EBG=90°,
∴在△EBG中,BE2+BG2=EG2,
即BE2+CF2=EF2.
∴∠DBG=∠DCF,
∵D是BC的中点,
∴BD=CD,
在△BGD和△CFD中,
|
∴△BGD≌△CFD(ASA),
∴BG=CF.
(2)BE2+CF2=EF2;
∵△BGD≌△CFD,
∴GD=FD,BG=CF,
又∵DE⊥FG,
∴EG=EF(垂直平分线上的点到线段两端点的距离相等),
∵∠A=90°,AC∥BG,
∴∠EBG=90°,
∴在△EBG中,BE2+BG2=EG2,
即BE2+CF2=EF2.
点评:本题考查了平行线的性质,三角形全等的判定和性质,线段的垂直平分线的性质以及勾股定理的应用,熟练掌握性质定理是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
下列说法正确的是( )
| A、带根号的数都是无理数 |
| B、无限小数都是无理数 |
| C、两个无理数之和一定是无理数 |
| D、两个无理数之积不一定是无理数 |
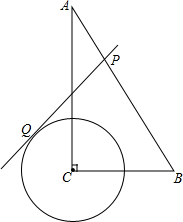 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为 如图,已知平面上有四个点A,B,C,D四个村庄.
如图,已知平面上有四个点A,B,C,D四个村庄.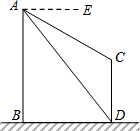 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.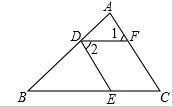 如图所示,点D,E,F分别在AB,BC,AC上.
如图所示,点D,E,F分别在AB,BC,AC上.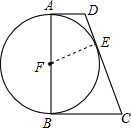 如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.
如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.