题目内容
根据所给x、y的值,求代数式(x+y)2+2(x+y)+1的值:
①x=
,y=
;
②x=
,y=
;
③x=-4,y=6;
④x=2,y=0.
观察题中第①~④小题计算结果有什么特点,并分析原因,请你再给2组x、y的值,使计算结果仍然保持上述特点.
①x=
| 1 |
| 2 |
| 3 |
| 2 |
②x=
| 3 |
| 2 |
| 1 |
| 2 |
③x=-4,y=6;
④x=2,y=0.
观察题中第①~④小题计算结果有什么特点,并分析原因,请你再给2组x、y的值,使计算结果仍然保持上述特点.
考点:代数式求值
专题:
分析:把(x+y)看作整体,先化简,再求值.
解答:解:(x+y)2+2(x+y)+1
=(x+y+1)2
①∵x=
,y=
,则x+y+1=3,
∴原式=32=9;
②∵x=
,y=
,则x+y+1=3,
∴原式=32=9;
③∵x=-4,y=6;则x+y+1=3,
∴原式=32=9;
④∵x=2,y=0则x+y+1=3,
∴原式=32=9;
观察题中第①~④小题计算结果相同,原因是x+y的值是定值2,
如x=2002,y=-2000,x+y+1=3,原式=32=9,
x=4,y=-2,x+y+1=3,原式=32=9,
=(x+y+1)2
①∵x=
| 1 |
| 2 |
| 3 |
| 2 |
∴原式=32=9;
②∵x=
| 3 |
| 2 |
| 1 |
| 2 |
∴原式=32=9;
③∵x=-4,y=6;则x+y+1=3,
∴原式=32=9;
④∵x=2,y=0则x+y+1=3,
∴原式=32=9;
观察题中第①~④小题计算结果相同,原因是x+y的值是定值2,
如x=2002,y=-2000,x+y+1=3,原式=32=9,
x=4,y=-2,x+y+1=3,原式=32=9,
点评:本题考查了代数式的求值,当代数式中,某个部分完全相同时,可把这个部分看作整体进行化简.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,在△ABC中,点D是∠ABC的平分线与∠ACB的外角平分线的交点,DE∥BC,交AB于E,交AC于F.
如图,在△ABC中,点D是∠ABC的平分线与∠ACB的外角平分线的交点,DE∥BC,交AB于E,交AC于F.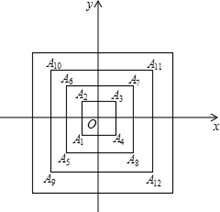 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A2014的坐标是
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A2014的坐标是