题目内容
7.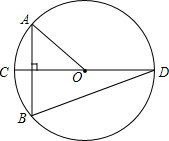 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.
分析 连接OB,先根据⊙O的直径CD垂直于AB得出$\widehat{BC}$=$\widehat{AC}$,由等弧所对的圆周角相等可知∠BOC=∠AOC,再根据圆周角定理即可得出结论.
解答  解:连接OB,
解:连接OB,
∵⊙O的直径CD垂直于AB,
∴$\widehat{BC}$=$\widehat{AC}$,
∴∠BOC=∠AOC=40°,
∴∠BDC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×40°=20°.
故答案为:20°.
点评 本题考查的是圆周角定理及垂径定理,根据题意得出$\widehat{BC}$=$\widehat{AC}$是解答此题的关键.

练习册系列答案
相关题目
17.若将分式$\frac{a+b}{ab}$(a,b均为正数)中a,b的值分别扩大为原来的3倍,则分式的值( )
| A. | 扩大为原来的3倍 | B. | 缩小为原来的$\frac{1}{3}$ | C. | 不变 | D. | 缩小为原来的$\frac{1}{9}$ |
2.下列计算正确的是( )
| A. | 2a+3a=6a | B. | a2+a3=a5 | C. | a8÷a2=a6 | D. | (a3)4=a7 |