题目内容
18.某商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价1元时,平均每天可多卖出2件.若商场要求该服装部每天盈利1200元,每件衬衫应降价多少元?分析 本题的关键语“每件降价1元时,平均每天可多卖出2件”,设每件应降价x元,用x来表示出商场所要求的每件盈利的数额量,然后根据盈利1200元来列出方程;
解答 解:设每件应降价x 元,由题意可列方程为(40-x )(30+2x )=1200,
解得x1=0,x2=25,
当x=0 时,能卖出30 件;
当x=25 时,能卖出80件,
根据题意,x=25 时能卖出80 件,符合题意,不降价也能盈利1200元,符合题意,
因为要减少库存,所以应降价25 元,
答:每件衬衫应降价25元;
点评 本题主要考查一元二次方程的应用,关键在于理解清楚题意找出等量关系列出方程求解,此题问题更是中考的热点考题之一,难度不大.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
10.如果(x+1)(2x+m)的乘积中不含x的一次项,则m的值为( )
| A. | 2 | B. | -2 | C. | 0.5 | D. | -0.5 |
8.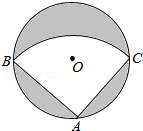 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )| A. | $\frac{{\sqrt{2}}}{2}$米 | B. | $\frac{{\sqrt{2}}}{4}$米 | C. | $\frac{1}{2}$米 | D. | $\frac{1}{4}$米 |

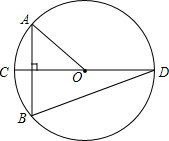 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.