题目内容
15.你会求(a-1)(a2012+a2011+a2010+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:$\begin{array}{l}(a-1)(a+1)={a^2}-1\\(a-1)({a^2}+a+1)={a^3}-1\\(a-1)({a^3}+{a^2}+a+1)={a^4}-1\end{array}$
(1)由上面的规律我们可以大胆猜想,得到(a-1)(a2014+a2013+a2012+…+a2+a+1)=a2015-1
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是22015-1.
(3)求52014+52013+52012+…+52+5+1的值.
分析 (1)根据已知算式得出规律,即可得出答案;
(2)先变形,再根据规律得出答案即可;
(3)先变形,再根据算式得出即可.
解答 解:(1)(a-1)(a2014+a2013+a2012+…+a2+a+1)
=a2015-1,
故答案为:a2015-1;
(2)22014+22013+22012+…+22+2+1
=(2-1)×(22014+22013+22012+…+22+2+1)
=22015-1,
故答案为:22015-1;
(3)52014+52013+52012+…+52+5+1
=$\frac{1}{4}$×(5-1)×(52014+52013+52012+…+52+5+1)
=$\frac{{5}^{2015}-1}{4}$.
点评 本题考查了整式的混合运算的应用,能根据题目中的算式得出规律是解此题的关键,难度适中.

练习册系列答案
相关题目
10.如果(x+1)(2x+m)的乘积中不含x的一次项,则m的值为( )
| A. | 2 | B. | -2 | C. | 0.5 | D. | -0.5 |
20. 如图,下列关于数m、n的说法正确的是( )
如图,下列关于数m、n的说法正确的是( )
 如图,下列关于数m、n的说法正确的是( )
如图,下列关于数m、n的说法正确的是( )| A. | m>n | B. | m=n | C. | m>-n | D. | m=-n |
4. 如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
 如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )| A. | $\left\{\begin{array}{l}x≥-2\\ x>3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<-2\\ x≤3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<-2\\ x≥3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>-2\\ x≤3\end{array}\right.$ |
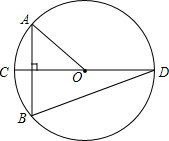 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.