题目内容
13.若a、b为实数,且$\frac{(a-2)^{2}+|{b}^{2}-16|}{b+4}$=0,求3a-b的值.分析 首先利用分式为0的条件和平方以及绝对值的性质得出a,b的值,进而代入3a-b求出即可.
解答 解:∵$\frac{(a-2)^{2}+|{b}^{2}-16|}{b+4}$=0,
∴$\left\{\begin{array}{l}{a-2=0}\\{{b}^{2}-16=0}\\{b+4≠0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$,
∴3a-b=6-4=2.
故3a-b的值是2.
点评 此题主要考查了绝对值和平方的性质,正确求出a,b的值是解题关键.

练习册系列答案
相关题目
8.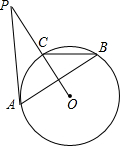 如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
 如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )| A. | 26° | B. | 64° | C. | 32° | D. | 90° |
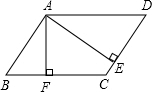 如图,在?ABCD中,AE⊥CD,AF⊥BC,垂足分别为E,F,∠EAF=60°,CE=1,CF=4.求?ABCD各边长.
如图,在?ABCD中,AE⊥CD,AF⊥BC,垂足分别为E,F,∠EAF=60°,CE=1,CF=4.求?ABCD各边长.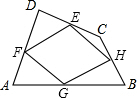 如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.
如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.