题目内容
9.在实数范围内因式分解(1)x2-7;
(2)4a4-9.
分析 根据平方差公式,可得答案.
解答 解:原式=x2-($\sqrt{7}$)2=(x+$\sqrt{7}$)(x-$\sqrt{7}$);
原式=(2a2+7)(2a2-7)
=(2a2+7)($\sqrt{2}$a+$\sqrt{7}$)($\sqrt{2}$a-$\sqrt{7}$).
点评 本题考查了因式分解,利用平方差公式是解题关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.若a<-$\sqrt{80}$<b(a,b是相邻的整数),则$\sqrt{\frac{ab}{8}}$的平方根为( )
| A. | $\sqrt{3}$ | B. | ±$\sqrt{3}$ | C. | 3 | D. | ±3 |
18.从A地到B地有许多条路,一般地,人们会从直路上通过,而不会走曲折的路,这是因为( )
| A. | 两点之间线段最短 | B. | 两直线相交只有一个交点 | ||
| C. | 两点确定一条直线 | D. | 不能确定 |
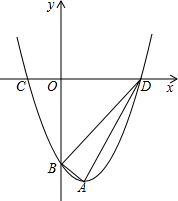 如图,抛物线y=x2-2x-3的顶点为A,与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状.
如图,抛物线y=x2-2x-3的顶点为A,与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状. 如图是一个抛物线形拱桥,量得两个数据,则会以抛物线顶点为原点建立直角坐标系,并求得其解析式为y=-0.03x2.
如图是一个抛物线形拱桥,量得两个数据,则会以抛物线顶点为原点建立直角坐标系,并求得其解析式为y=-0.03x2. 如图所示,AB∥CD,∠1=∠4,求证:EG∥FH.
如图所示,AB∥CD,∠1=∠4,求证:EG∥FH.