题目内容
15．已知x2-4x+1=0，求（1）x2+$\frac{1}{{x}^{2}}$；（2）x3+$\frac{1}{{x}^{3}}$．分析 （1）将已知条件进行变形得到x+$\frac{1}{x}$=4，由完全平方公式得到x2+$\frac{1}{{x}^{2}}$=14；
（2）根据（1）的结论然后利用立方和公式进行计算即可．
解答 解：（1）∵x2-4x+1=0，
∴x+$\frac{1}{x}$=4，
∴x2+$\frac{1}{{x}^{2}}$=（x+$\frac{1}{x}$）2-2=14；
（2）x3+$\frac{1}{{x}^{3}}$=（x+$\frac{1}{x}$）（x2-1+$\frac{1}{{x}^{2}}$）=52．
点评 本题考查了完全平方公式，立方和公式，熟记公式是解题的关键．
练习册系列答案
相关题目
5．下列各式合并同类项正确的是（ ）
| A． | x+2x=3x2 | B． | 2m+3n=5mn | C． | 5a4-2a2=3a2 | D． | 3x2y-2yx2=x2y |
如图，在△ABC中，AB=AD=CD，∠CAD-∠BAD=10°，求∠B和∠C的度数．
如图，一个圆锥的母线AB=2.5cm，底面半径OB=0.7cm，求它的高AO．
如图，直线AC，DE相交于点O，OE是∠AOB的平分线，∠COD=50°．试求∠AOB的度数．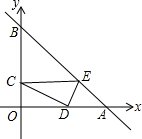
如图，点A的坐标是（4，0），B的坐标是（0，4），点C在射线OB上，过点C作CE∥x轴交直线AB于点E，D为x轴正半轴上的一点，OD=2OC，连接CD，DE，设OC=m．