题目内容
20．
如图，在△ABC中，AB=AD=CD，∠CAD-∠BAD=10°，求∠B和∠C的度数．
分析 由题意，在△ABC中，AB=AD=DC，∠CAD-∠BAD=10°，根据等腰三角形的性质可以求出底角，再根据三角形内角与外角的关系即可求出内角∠C．
解答 解：在△ABC中，AB=AD=DC，
∵AB=AD，在三角形ABD中，
∴∠B=∠ADB=$\frac{1}{2}$（180°-∠BAD），
∴∠BAD=180°-2∠B，
又∵AD=DC，在三角形ADC中，
∴∠C=∠CAD=$\frac{1}{2}$∠ADB=$\frac{1}{2}∠$B，
∵∠CAD-∠BAD=10°，
∴$\frac{1}{2}$∠B-（180°-2∠B）=10°，
∴∠B=72°，
∴∠C=36°．
点评 本题考查等腰三角形的性质及应用等腰三角形两底角相等，还考查了三角形的内角和定理及内角与外角的关系．利用三角形的内角求角的度数是一种常用的方法，要熟练掌握．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
11．
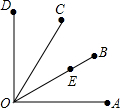如图所示，OA=OB=OC=OD=10．点E在OB上且BE=3，∠A0B=∠BOC=∠COD=30°，若点B的位置是（30°，10）．点C的位置是（60°，10），点D的位置是（90°，10），则点E的位置是（ ）
如图所示，OA=OB=OC=OD=10．点E在OB上且BE=3，∠A0B=∠BOC=∠COD=30°，若点B的位置是（30°，10）．点C的位置是（60°，10），点D的位置是（90°，10），则点E的位置是（ ）| A． | （30°，3） | B． | （30°，7） | C． | （60°，3） | D． | （60°，7） |
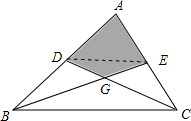如图，在△ABC中，中线CD，BE交于点G，已知△ABC的面积等于4，求四边形ADGE的面积．