题目内容
13．
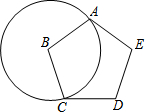如图所示，正五边形ABCDE的边长为1，⊙B过五边形的顶点A、C，扇形ABC可以围成一个圆锥的侧面，则该圆锥的侧面积为$\frac{3}{10}$π．
分析 由正五边形的性质好内角和定理得出∠B=108°，然后由扇形的面积公式即可得出结果．
解答 解：∵五边形ABCDE是正五边形，
∴∠B=$\frac{1}{5}$（5-2）×180°=108°，
∴扇形的面积=$\frac{108π×{1}^{2}}{360}$=$\frac{3}{10}$π；
故答案为：$\frac{3}{10}$π．
点评 本题考查了正五边形的性质、多边形内角和定理、弧长公式；熟练掌握正五边形的性质，由内角和定理求出∠B的度数是解决问题的关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
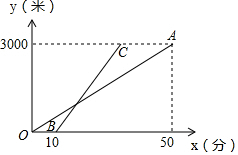波波和爸爸两人以相同路线从家出发，步行前往公园．图中OA、BC分别表示爸爸和波波所走的路程y（米）与爸爸步行的时间x（分）的函数图象，已知爸爸从家步行到公园所花的时间比波波的2倍还多10分钟．则在步行过程中，他们父子俩相距的最远路程是1200米．
如图，在△ABC中，AB=AC=10，BC=12，BD是高，则BD的长为9.6．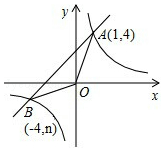
如图，反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于点A（1，4）、点B（-4，n）．
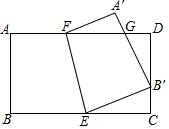如图，矩形ABCD中，AD=5，E、F分别是BC、AD边上的点，AF=x，四边形ABEF沿EF翻折至A′B′EF，点B′恰好落在边CD上，A′B′与AD相交于点G，△B′GD≌△FGA′．