题目内容
2.若关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$有增根,则该方程的增根为0或3.分析 增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母x(x-3)=0,得到x=0或3.
解答 解:∵原方程有增根,
∴最简公分母x(x-3)=0,
解得x=0或3.
故答案为:0或3.
点评 本题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
10.方程3(x-3)2=2(x-3)的根是( )
| A. | x=3 | B. | x=$\frac{11}{3}$ | C. | x1=3,x2=$\frac{2}{3}$ | D. | x1=3,x2=$\frac{11}{3}$ |
14.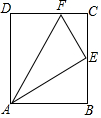 折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )
折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )
 折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )
折叠矩形ABCD,使点D落在BC的边上点E处,并使折痕经过点A交CD于点F,若点E恰好为BC的中点,则CE:CF等于( )| A. | $\sqrt{3}$:1 | B. | 5:2 | C. | $\sqrt{2}$:1 | D. | 2:1 |
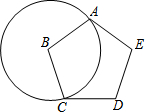 如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,扇形ABC可以围成一个圆锥的侧面,则该圆锥的侧面积为$\frac{3}{10}$π.
如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,扇形ABC可以围成一个圆锥的侧面,则该圆锥的侧面积为$\frac{3}{10}$π.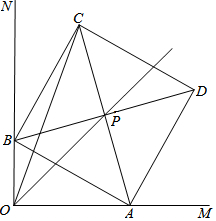 已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.
已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.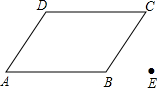 平移图中平行四边形的A点至E点,并作出平移后的平行四边形.
平移图中平行四边形的A点至E点,并作出平移后的平行四边形. 如图所示,PA、PB切⊙O于点A、B,连接AB交直线OP于点C,若⊙O的半径为3,PA=4,则OC的长为$\frac{9}{5}$.
如图所示,PA、PB切⊙O于点A、B,连接AB交直线OP于点C,若⊙O的半径为3,PA=4,则OC的长为$\frac{9}{5}$.