题目内容
18.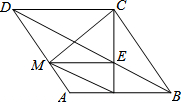 己知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.
己知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.(1)求证:DM=BN;
(2)当四边形MNBE是平行四边形时,求证:$\frac{DM}{MA}$=$\frac{DC}{DM}$.
分析 (1)在菱形ABCD中,根据菱形的性质得到CD=BC,∠CDM=∠CBN,推出△CDM≌△CBN,于是得到结论;
(2)根据平行四边形的性质得到ME∥AB,由平行线分线段成比例得到$\frac{DM}{AM}=\frac{DE}{EB}$,由△CDE∽△NBE,得到$\frac{DE}{BE}$=$\frac{CD}{BN}$,等量代换即可得到结论.
解答 (1)证明:在菱形ABCD中,
∵CD=BC,∠CDM=∠CBN,
在△CDM与△CBN中,$\left\{\begin{array}{l}{∠CDM=∠CBN}\\{CD=CB}\\{∠DCM=∠BCN}\end{array}\right.$,
∴△CDM≌△CBN,
∴DM=BN;
(2)解:∵四边形MNBE是平行四边形,
∴ME∥AB,
∴$\frac{DM}{AM}=\frac{DE}{EB}$,
∵DC∥AB
∴△CDE∽△NBE,
∴$\frac{DE}{BE}$=$\frac{CD}{BN}$,
∴$\frac{DM}{AM}=\frac{CD}{NB}$,
∵DM=NB,
∴$\frac{DM}{MA}$=$\frac{DC}{DM}$.
点评 本题考查了相似三角形的判定和性质,菱形的性质,平行四边形的性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.下面的图案是由一个图形经过多次轴对称变换得到的,在这些对称轴中,共有平行线( )

| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 自然数中从1开始,按从小到大的顺序排列成螺旋形.在2处拐第一个弯,在3处拐第二个弯,在5处拐第三个弯,…,问拐第20个弯的地方是哪一个数?
自然数中从1开始,按从小到大的顺序排列成螺旋形.在2处拐第一个弯,在3处拐第二个弯,在5处拐第三个弯,…,问拐第20个弯的地方是哪一个数?