题目内容
1．
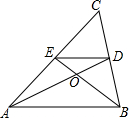如图，在△ABC中，AD、BE是两条中线，则S△DOB：S△AOB=（ ）| A． | 1：2 | B． | 2：3 | C． | 1：3 | D． | 1：4 |
分析 根据三角形的中位线得出DE∥AB，DE=$\frac{1}{2}$AB，根据平行线的性质得出相似，根据相似三角形的性质求出即可．
解答 解：∵AD、BE是两条中线，
∴DE=$\frac{1}{2}$AB，DE∥AB，
∴$\frac{DE}{AB}$=$\frac{1}{2}$，△DOE∽△COB，
∴S△DOB：S△AOB=（$\frac{DE}{AB}$）2=（$\frac{1}{2}$）2=$\frac{1}{4}$，
故选：D．
点评 本题考查了相似三角形的性质和判定，三角形的中位线的应用，注意：相似三角形的面积比等于相似比的平方，三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
相关题目
如图，一次函数y=$\frac{\sqrt{3}}{3}$x+b的图象与x轴相交于点A（5$\sqrt{3}$，0），与y轴相交于点B
16．
如图所示，同位角共有（ ）对．
如图所示，同位角共有（ ）对．| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
自然数中从1开始，按从小到大的顺序排列成螺旋形．在2处拐第一个弯，在3处拐第二个弯，在5处拐第三个弯，…，问拐第20个弯的地方是哪一个数？
13．下面的图案是由一个图形经过多次轴对称变换得到的，在这些对称轴中，共有平行线（ ）
| A． | 1组 | B． | 2组 | C． | 3组 | D． | 4组 |
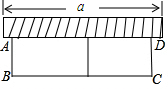如图，有一个长为24米的篱笆，一面利用墙（墙的最大长度a为15米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．