题目内容
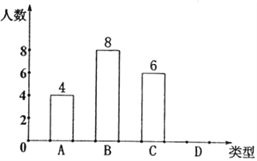
【题目】某校260名学生参加献爱心捐款活动,每人捐款4~7元,活动结束后随机抽查了20名学生每人的捐款数量,并按每人的捐款数量分为四种类型,A:捐款4元;B:捐款5元;C:捐款6元;D:捐款7元,并将其绘成如图所示的条形统计图.
(1)通过计算补全条形统计图;
(2)直接写出这20名学生每人捐款数量的众数和中位数;
(3)求这20名学生每人捐款数量的的平均数,并估计260名学生共捐款多少元.
【答案】(1)见解析(2)5元 5元(3) 1378元
【解析】试题分析:(1)利用20减去其它组的人数即可求得D组的人数,从而补全条形图;
(2)根据众数、中位数的定义即可求解;
(3)利用加权平均数公式求得抽查的20人的捐款数,乘以260即可求解.
试题解析:(1)20-4-8-6=2(名),
补全条形统计图如图所示;

(2)捐款5元的人数最多,故众数:5元,
20个数据中位数是第10个与第11个数据的平均数,因为4<10,4+8=12>11,
所以中位数落在B捐款5元这一组,所以中位数:5元;
(3)![]() =5.3(元),
=5.3(元),
5.3×260=1378(元),
答:这20名学生每人捐款数量的的平均数是5.3元,估计260名学生共捐款1378元.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
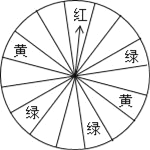
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?