Question

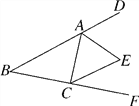
【题目】如图，四边形ABCD是⊙O的内接四边形，点F 是CD延长线上的一点，且AD平分∠BDF，AE⊥CD于点E.

⑴ 求证：AB＝AC.

⑵ 若BD＝11，DE＝2，求CD的长.

Answer 1

【答案】⑴ 证明见解析⑵ 7

【解析】试题分析：（1）同弧所对圆周角相等∠BCA=∠ADB,四边形的外接圆性质，可以得∠ADF=∠ABC,利用AD平分∠BDF,可以得到AB=AC.

(2)试题解析：过A作BD的垂线于G，构造两个全等三角形，

GD＝ED,BG＝CE ,可得CD长.

试题解析：

⑴ ∵ AD平分∠BDF ，

∴ ∠ADF＝∠ADB，

∵ ∠ABC＋∠ADC＝180°，∠ADC＋∠ADF＝180°，

∴ ∠ADF＝∠ABC,

∵ ∠ACB＝∠ADB,

∴ ∠ABC＝∠ACB,

∴ AB＝AC .

⑵ 过点A作AG⊥BD，垂足为点G.

∵ AD平分∠BDF，AE⊥CF，AG⊥BD.

∴ AG＝AE，∠AGB＝∠AEC＝90°，

在Rt△AED和Rt△AGD中,

,

∴ Rt△AED≌Rt△AGD（HL）,

∴ GD＝ED＝2,

在Rt△AEC和Rt△AGB中,

,

∴ Rt△AEC≌Rt△AGB（HL）,

∴ BG＝CE ,

∵ BD＝11,

∴ BG＝BD－GD＝11－2＝9 .

∴ CE＝BG＝9.

∴ CD＝CD－DE＝9－2＝7.