题目内容
【题目】阅读与理解:
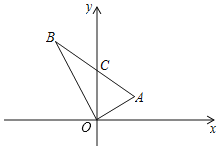
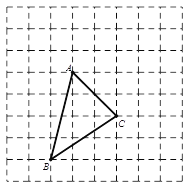
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
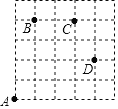
(1)图中B→C( , )C→D( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程S.
【答案】(1)+2,0,+1,﹣2;(2)若甲虫从A到P的行走路线依次为:A→E→F→P,图中P的即为所求.见解析;(3)甲虫走过的总路程为16.
【解析】
(1)B→C只向右走3格;C→D先向右走1格,再向下走2格,由此写出即可.
(2)由(+3,+2)→(+1,+3)→(+1,﹣2)可知从A处右移3格,上移2格,再右移1格,上移3格,右移1格,下移2格即是甲虫P处的位置;
(3)由A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2)知:先向右移动1格,向上移动4格,向右移动2格,再向右移动1格,向下移动2格,最后向左移动4格,向下移动2格,把移动的距离相加即可.
(1)图中B→C(+2.0),C→D(+1,﹣2).
故答案为:+2,0,+1,﹣2.
(2)若甲虫从A到P的行走路线依次为:A→E→F→P,图中P的即为所求.
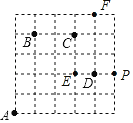
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),
甲虫走过的总路程S=1+4+2+1+2+4+2=16.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.