Question

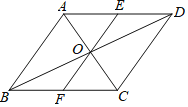
【题目】如图，过平行四边形ABCD对角线交点O的线段EF，分别交AD，BC于点E，F，当AE＝ED时，△AOE的面积为4，则四边形EFCD的面积是（　　）

A.8B.12C.16D.32

Answer 1

【答案】C

【解析】

根据等底等高的三角形面积相等可得S△DOE＝S△AOE＝4，进而可得S△COD＝S△AOD＝8，再由平行四边形性质可证明△COF≌△AOE（ASA），S△COF＝S△AOE＝4，即可得S四边形EFCD＝16．

解：∵ABCD是平行四边形，∴AD∥BC，AD＝BC，AO＝CO，OB＝OD

∴∠DAC＝∠ACB，

∵∠AOE＝∠COF

∴△COF≌△AOE（ASA）

∵S△AOE＝4，AE＝ED

∴S△COF＝S△DOE＝S△AOE＝4，

∴S△AOD＝8

∵AO＝CO

∴S△COD＝S△AOD＝8

∴S四边形EFCD＝S△DOE+S△COD+S△COF＝4+8+4＝16；

故选：C．