题目内容
12．
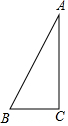△ABC中，∠C=90°，∠B=60°，AC=3，以C为圆心，r为半径作⊙C，如果点B在圆内，而点A在圆外，那么r的取值范围是$\sqrt{3}$＜r＜3．
分析 根据直角三角形的角的度数和AC的长可以求出BC的长，然后由点B在圆内，点A在圆外，确定r的取值范围．
解答 解：因为△ABC中，∠C=90°，∠B=60°，所以∠A=30°，得到AC=$\sqrt{3}$BC，又AC=3，得BC=$\sqrt{3}$，
∵点B在圆内，∴r＞BC=$\sqrt{3}$，
∵点A在圆外，∴r＜AC=3．
因此：$\sqrt{3}$＜r＜3．
故答案是：$\sqrt{3}$＜r＜3．
点评 本题考查的是点和圆的位置关系，先求出三角形的BC边的长，再根据点B和点A与⊙C的位置关系确定半径的取值范围．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
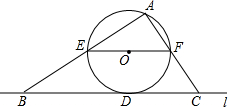如图，直线l与⊙相切于点D，过圆心O作EF∥l交⊙O于E、F两点，点A是⊙O上一点，连接AE，AF，并分别延长交直线于B、C两点；若⊙的半径R=5，BD=12，则∠ACB的正切值为$\frac{7}{5}$．
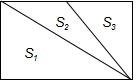如图是由三个三角形组成的一个面积为（6a2+4a）cm2的长方形，三个三角形的面积分别是S1，S2，S3，若S1=（3a2+2a）cm2，S3=（2a2-a）cm2，则S2等于（a2+3a）cm2．
如图，∠3和∠9是直线AD、BD被直线AC所截而成的同位角；∠6和∠9是直线BC、AC被直线BD所截而成的同位角．