题目内容
2.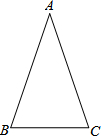 如图,在△ABC中,AB=AC,∠A=36°,且BC=2,则AB=$\sqrt{5}+1$.
如图,在△ABC中,AB=AC,∠A=36°,且BC=2,则AB=$\sqrt{5}+1$.
分析 作∠ABC的平分线交AC于D如图,根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠C=72°,则∠ABD=∠CBD=36°,所以DA=DB,易得BD=BC,则AD=BC,再证明△BCD∽△ABC,得到BC2=CD•AD,则AD2=CD•AD,根据黄金分割的定义得到点D为AC的黄金分割点,据此可得AB的长.
解答 解:如图,作∠ABC的平分线交AC于D,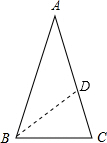
∵AB=AC,且∠A=36°,
∴∠ABC=∠C=72°,
∴∠ABD=∠CBD=36°,
∴DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC,
∵∠CBD=∠A,∠BCD=∠ACB,
∴△BCD∽△ABC,
∴BC:AC=CD:BC,
∴BC2=CD•AD,
∴AD2=CD•AD,
∴点D为AC的黄金分割点,
∴$\frac{AD}{AC}$=$\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$,
即$\frac{2}{AC}$=$\frac{\sqrt{5}-1}{2}$,
∴AC=$\sqrt{5}+1$=AB,
故答案为:$\sqrt{5}+1$.
点评 本题考查了黄金分割,解题时注意:若点C把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,点C叫做线段AB的黄金分割点,其中AC=$\frac{\sqrt{5}-1}{2}$AB,线段AB的黄金分割点有两个.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知反比例函数y=-$\frac{4}{x}$,则下列有关该函数的说法正确的是( )
| A. | 该函数的图象经过点(2,2) | B. | 该函数的图象位于第一、三象限 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x>-1时,y>4 |
7.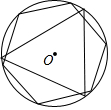 图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
 图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )
图中的正三角形和正六边形有公共的外接圆⊙O.则这个正三角形和正六边形边长的比为( )| A. | $\sqrt{6}$:2 | B. | $\sqrt{3}$:2 | C. | $\sqrt{3}$:1 | D. | 2:1 |
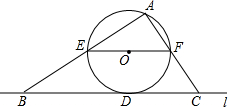 如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为$\frac{7}{5}$.
如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为$\frac{7}{5}$.