题目内容
20.计算:(1)$\sqrt{6}•\sqrt{12}÷\sqrt{75}$
(2)$\sqrt{12}+\sqrt{20}-(\sqrt{5}-\sqrt{3})$
(3)$\sqrt{50}+\sqrt{8}-4\sqrt{\frac{1}{2}}+2{(\sqrt{2}-1)^0}$;
(4)$({\sqrt{9a}+a\sqrt{\frac{1}{a}}-\frac{2}{a}\sqrt{a^3}})÷\sqrt{b}$.
分析 (1)首先化简二次根式进而利用二次根式乘除运算法则求出即可;
(2)首先化简二次根式进而利用二次根式加减运算法则求出即可;
(3)首先化简二次根式进而利用二次根式加减运算法则求出即可;
(4)首先化简二次根式进而利用二次根式加减运算法则求出即可.
解答 解:(1)$\sqrt{6}•\sqrt{12}÷\sqrt{75}$
=6$\sqrt{2}$÷5$\sqrt{3}$
=$\frac{6}{5}$×$\frac{\sqrt{6}}{3}$
=$\frac{2\sqrt{6}}{5}$;
(2)$\sqrt{12}+\sqrt{20}-(\sqrt{5}-\sqrt{3})$
=2$\sqrt{3}$+2$\sqrt{5}$-$\sqrt{5}$+$\sqrt{3}$
=3$\sqrt{3}$+$\sqrt{5}$;
(3)$\sqrt{50}+\sqrt{8}-4\sqrt{\frac{1}{2}}+2{(\sqrt{2}-1)^0}$
=5$\sqrt{2}$+2$\sqrt{2}$-2$\sqrt{2}$+2
=5$\sqrt{2}$+2;
(4)$({\sqrt{9a}+a\sqrt{\frac{1}{a}}-\frac{2}{a}\sqrt{a^3}})÷\sqrt{b}$
=(3$\sqrt{a}$+$\sqrt{a}$-2$\sqrt{a}$)÷$\sqrt{b}$
=$\frac{2}{b}\sqrt{ab}$.
点评 此题主要考查了二次根式的混合运算,正确利用化简二次根式再计算是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.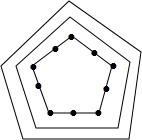 在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
 在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
在一次大型演出中,由1200名演员排出如图所示的正五边形队,内圈每边3人,往外每圈每边增加2人(即由内向外算起,第2圈每边5人,第三圈每边7人…),这样1200人恰好排完,则这个队共排了15圈.
11. 如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
 如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )
如图,把图中的一个三角形先横向平移x格,再纵向平移y格,可以与图中另一个三角形拼合成一些不同的四边形,那么移动的总格数(x+y)的值是( )| A. | 是一个定值 | B. | 有两个不同的值 | ||
| C. | 有三个不同的值 | D. | 有三个以上不同的值 |
8.下列运算正确的是( )
| A. | 32-2a2=1 | B. | a6÷a3=a2 | C. | (a-b)2=a2-b2 | D. | 2a•4a=8a2 |
15. 如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
 如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )| A. | 13个 | B. | 14个 | C. | 15个 | D. | 16个 |
5.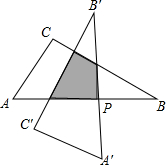 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为( )| A. | $\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\frac{9}{4}$ | D. | $\frac{15}{4}$ |
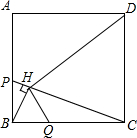 如图,P、Q是正方形ABCD边AB、BC上的点,BH⊥PC,垂足为H,且DH⊥HQ.
如图,P、Q是正方形ABCD边AB、BC上的点,BH⊥PC,垂足为H,且DH⊥HQ.