题目内容
18.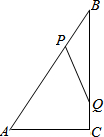 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.若△BPQ与△ABC相似,则t的值为1秒或$\frac{32}{41}$秒.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.若△BPQ与△ABC相似,则t的值为1秒或$\frac{32}{41}$秒.
分析 设运动时间为t秒(0<t<2),则BP=5t,CQ=4t,BQ=8-4t,先利用勾股定理计算出AB=10,分类讨论:当△BPQ∽△BAC时,根据相似三角形的性质得$\frac{5t}{10}$=$\frac{8-4t}{8}$;当△BPQ∽△BQP,根据相似三角形的性质得$\frac{5t}{8}$=$\frac{8-4t}{10}$,然后分别解方程求出t的值即可.
解答 解:设运动时间为t秒(0<t<2),则BP=5t,CQ=4t,BQ=8-4t,
∵∠ACB=90°,AC=6,BC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
当△BPQ∽△BAC时,$\frac{BP}{BA}$=$\frac{BQ}{BC}$,即$\frac{5t}{10}$=$\frac{8-4t}{8}$,解得t=1(秒);
当△BPQ∽△BQP时,$\frac{BP}{BC}$=$\frac{BQ}{BA}$,即$\frac{5t}{8}$=$\frac{8-4t}{10}$,解得t=$\frac{32}{41}$(秒),
即当t=1秒或$\frac{32}{41}$秒时,△BPQ与△ABC相似.
故答案为1秒或$\frac{32}{41}$秒时
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等.也考查了分类讨论的思想和利用代数法解决动点问题.

练习册系列答案
相关题目
3.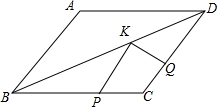 如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,△ABD≌△CDB,且∠ADB=∠ABD,△ABD的面积是2$\sqrt{3}$,AB=2,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2 | D. | 2$\sqrt{3}$ |
 如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是$\sqrt{30}$m.
如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是$\sqrt{30}$m. 如图,在四边形ABCD内选一点O为位似中心将它放大为原来的两倍(保留作图痕迹).
如图,在四边形ABCD内选一点O为位似中心将它放大为原来的两倍(保留作图痕迹).