题目内容
9. 如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是$\sqrt{30}$m.
如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是$\sqrt{30}$m.
分析 首先连接AO,求出AB的长度是多少;然后求出扇形的弧长$\widehat{BC}$为多少,进而求出扇形围成的圆锥的底面半径是多少;最后应用勾股定理,求出圆锥的高是多少即可.
解答 解:如图1,连接AO,
∵AB=AC,点O是BC的中点,
∴AO⊥BC,
又∵∠BAC=90°,
∴∠ABO=∠AC0=45°,
∴AB=$\sqrt{2}$OB=4$\sqrt{2}$(m),
∴$\widehat{BC}$=$\frac{90}{360}$×2π×4$\sqrt{2}$=2$\sqrt{2}$π(m),
∴将剪下的扇形围成的圆锥的半径是:
2$\sqrt{2}$π÷2π=$\sqrt{2}$(m),
∴圆锥的高是:$\sqrt{(4\sqrt{2})^{2}-(\sqrt{2})^{2}}$=$\sqrt{30}$(m).
故答案为:$\sqrt{30}$.
点评 此题主要考查了圆锥的计算,要熟练掌握,解答此题的关键是求出扇形围成的圆锥的底面半径是多少.

练习册系列答案
相关题目
20.下列结论不正确的是( )
| A. | 若a+2=b+2,则a=b | B. | 若ac=bc,则a=b | ||
| C. | 若ax=b(a≠0),则x=$\frac{b}{a}$ | D. | 若$\frac{a}{c}=\frac{b}{c}$,则a=b |
4.长为9,6,5,4,3的五根木棒,选其中三根组成三角形,选法是( )
| A. | 10种 | B. | 8种 | C. | 6种 | D. | 4种 |
19.下列说法错误的是( )
| A. | 倒数等于它本身的数有±1,0 | B. | 0不是正数,也不是负数 | ||
| C. | 绝对值最小的有理数是0 | D. | 有理数a相反数是-a |
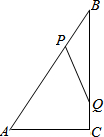 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.若△BPQ与△ABC相似,则t的值为1秒或$\frac{32}{41}$秒.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.若△BPQ与△ABC相似,则t的值为1秒或$\frac{32}{41}$秒.