题目内容
13.计算.①$\frac{{\sqrt{15}+\sqrt{60}}}{{\sqrt{3}}}-3\sqrt{5}$
②${({\sqrt{2}-\sqrt{3}})^2}+2\sqrt{\frac{1}{3}}×3\sqrt{2}$.
分析 ①首先利用多项式与单项式的除法法则计算,然后化简二次根式,合并同类二次根式即可;
②首先利用完全平方公式以及二次根式的乘法法则计算,然后化简二次根式,合并同类二次根式即可求解.
解答 解:①原式=$\sqrt{5}$+$\sqrt{20}$-3$\sqrt{5}$=$\sqrt{5}$+2$\sqrt{5}$-3$\sqrt{5}$=0;
②原式=2+3-2$\sqrt{6}$+6$\sqrt{\frac{2}{3}}$=5-2$\sqrt{6}$+2$\sqrt{6}$=5.
点评 本题考查的是二次根式的混合运算,在二次根式的混合运算中,要掌握好运算顺序及各运算律.

练习册系列答案
相关题目
4.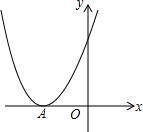 已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )
 已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )| A. | 有最小值-5、最大值0 | B. | 有最小值-3、最大值6 | ||
| C. | 有最小值0、最大值6 | D. | 有最小值2、最大值6 |
1.某商场在促销期间规定:商场对所有商品按标价的80%出售.同时当顾客在该商场消费满一定金额后,按如下方案获得响应金额的奖券:
根据上述促销方法,顾客在商场内购物可以获得双重的优惠额=折扣所享金额+奖券金额;设购买商品得到的优惠率=购买商品获得优惠额÷商品的标价.问:
(1)购买一件标价为1000元的商品,获得的优惠额为多少?优惠率是多少?
(2)对于标价在500元到800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到三分之一的优惠率?
| 消费金额a(元)的范围 | 200≤a<400 | 400≤a<500 | 500≤a<700 | 700≤a<900 | … |
| 获得奖券的金额 | 30 | 60 | 100 | 130 | … |
(1)购买一件标价为1000元的商品,获得的优惠额为多少?优惠率是多少?
(2)对于标价在500元到800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到三分之一的优惠率?
8.计算(-5$\frac{1}{7}$)2015•($\frac{7}{36}$)2016的结果是( )
| A. | $\frac{7}{36}$ | B. | $\frac{36}{7}$ | C. | -$\frac{7}{36}$ | D. | -$\frac{36}{7}$ |
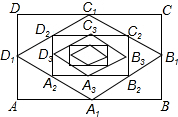 如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3,…这样继续下去.则图中的四边形A8B8C8D8的周长等于$\frac{7}{2}$,图中的四边形A9B9C9D9的面积等于$\frac{3}{8}$.
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3,…这样继续下去.则图中的四边形A8B8C8D8的周长等于$\frac{7}{2}$,图中的四边形A9B9C9D9的面积等于$\frac{3}{8}$. 如图,正方形ABCD与正方形CEFG(边长不等),B、C、F三点共线,连接BE交CD于M,连接DG交BE、CE、CF分别于N、P、Q,以下四个结论:①BE=DG;②BM=DQ;③CM=CP;④∠BNQ=90°恒成立的有①②④(把你认为正确的序号都填上).
如图,正方形ABCD与正方形CEFG(边长不等),B、C、F三点共线,连接BE交CD于M,连接DG交BE、CE、CF分别于N、P、Q,以下四个结论:①BE=DG;②BM=DQ;③CM=CP;④∠BNQ=90°恒成立的有①②④(把你认为正确的序号都填上).