题目内容
8. 平面直角坐标系中,△ABC的位置如图所示,已知OA=2OB,BC=5,△ABC的面积为5.
平面直角坐标系中,△ABC的位置如图所示,已知OA=2OB,BC=5,△ABC的面积为5.(1)求△ABC的三个顶点的坐标;
(2)若P(a,2)是第一象限内一点,且△PAC的面积等于△ABC的面积,求点P的坐标.
分析 (1)根据SABC=5、BC=5可得OA,即可知A的坐标,由OA=2OB可得OB,从而得出点B坐标,继而根据BC、OB的值得OC,知点C坐标;
(2)根据S△PAC=S直角梯形PAOC-S△AOC,用含a的式子表示出S△PAC,由S△PAC=S△ABC即可得答案.
解答 解:(1)∵S△ABC=$\frac{1}{2}$BC•OA,且SABC=5,BC=5,
∴5=$\frac{1}{2}$×5•OA,
∴OA=2,
∴点A坐标为(0,2),
∵OA=2OB,
∴OB=1,即点B坐标为(-1,0),
∵OC=BC-OB=4,
∴点C坐标为(4,0);
(2)如图,
∵P(a,2)是第一象限内一点,
∴S△PAC=S直角梯形PAOC-S△AOC=$\frac{1}{2}$(a+4)×2-$\frac{1}{2}$×2×4=a,
又∵S△PAC=S△ABC,且SABC=5,
∴a=5,
则P点坐标为(5,2).
点评 本题主要考查坐标与图形的性质及三角形面积的计算,熟练掌握割补法求三角形的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次连续行驶纪录如表.(单位:km)
(1)在第五次纪录时距A地最远.
(2)求收工时距A地多远?
(3)若行驶每km耗油0.4升,问共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +6 | -8 | +7 | +5 | -4 | -2 |
(2)求收工时距A地多远?
(3)若行驶每km耗油0.4升,问共耗油多少升?
 如图,点O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,连接OE.求证:
如图,点O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,连接OE.求证: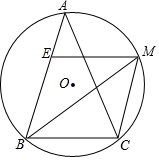 如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.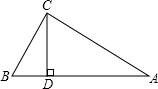 如图.在△ABC中,∠ACB=90°.CD是AB边上的高.∠A=30°.想一想:BD与AB有怎样的数量关系.
如图.在△ABC中,∠ACB=90°.CD是AB边上的高.∠A=30°.想一想:BD与AB有怎样的数量关系. 如图,在△ABC中,∠C=65°,∠ADB=85°,AD是△ABC的角平分线,求∠B的度数.
如图,在△ABC中,∠C=65°,∠ADB=85°,AD是△ABC的角平分线,求∠B的度数.