题目内容
3.如图,线段AC=6cm,线段BC=15cm,点M是AC的中点,在BC上取一点N,使得CN=$\frac{1}{3}$BC,求MN的长.
分析 根据线段中点的性质求出MC的长,根据题意列式求出CN的长,结合图形计算即可.
解答 解:∵M是AC的中点,
∴MC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm,
∵CN=$\frac{1}{3}$BC,
∴CN=$\frac{1}{3}$×15=5cm,
∴MN=MC+NC=3+5=8cm.
点评 本题考查的是两点间的距离的计算,掌握线段中点的性质、灵活运用数形结合思想是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.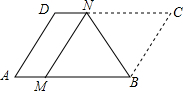 如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
 如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )| A. | ①②都错 | B. | ①对②错 | C. | ①错②对 | D. | ①②都对 |
13.人的眼睛可以看见的红光的波长是0.000077cm,用科学记数法表示为( )cm.
| A. | 0.77×10-6 | B. | 77×10-4 | C. | 7.7×10-5 | D. | 7.7×10-6 |
 一艘轮船与一艘快船沿相同方向行驶,轮船与快艇行驶过程中路程随时间变化的图象如图所示,请解答下列问题:
一艘轮船与一艘快船沿相同方向行驶,轮船与快艇行驶过程中路程随时间变化的图象如图所示,请解答下列问题: 四边形ABDC在如图所示的平面直角坐标系中,将四边形ABDC向右平移4个单位长度后得四边形A1B1D1C1,再将四边形ABDC绕点O旋转180°后得到四边形A2B2D2C2.
四边形ABDC在如图所示的平面直角坐标系中,将四边形ABDC向右平移4个单位长度后得四边形A1B1D1C1,再将四边形ABDC绕点O旋转180°后得到四边形A2B2D2C2. 将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是明.
将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是明. 如图,点B、D、C、F在一条直线上,BC=FD,AB=EF,且AB∥EF.求证:AC∥ED.
如图,点B、D、C、F在一条直线上,BC=FD,AB=EF,且AB∥EF.求证:AC∥ED.