题目内容
 如图,∠A+∠B+∠C+∠D+∠E=
如图,∠A+∠B+∠C+∠D+∠E=考点:三角形内角和定理
专题:
分析:先根据三角形外角的性质得出∠CFB=∠A+∠C,∠BGF=∠D+∠E,再由三角形内角和定理即可得出结论.
解答: 解:∵∠CFB是△ACF的外角,∠BGF是△DEG的外角,
解:∵∠CFB是△ACF的外角,∠BGF是△DEG的外角,
∴∠CFB=∠A+∠C,∠BGF=∠D+∠E,
∵∠B+∠CFB+∠BGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
 解:∵∠CFB是△ACF的外角,∠BGF是△DEG的外角,
解:∵∠CFB是△ACF的外角,∠BGF是△DEG的外角,∴∠CFB=∠A+∠C,∠BGF=∠D+∠E,
∵∠B+∠CFB+∠BGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题:
①若b=2a+
c,则一元二次方程ax2+bx+c=O必有一根为-2;
②若ac<0,则方程cx2+bx+a=O有两个不等实数根;
③若b2-4ac=0,则方程cx2+bx+a=O有两个相等实数根.
其中正确的个数是( )
①若b=2a+
| 1 |
| 2 |
②若ac<0,则方程cx2+bx+a=O有两个不等实数根;
③若b2-4ac=0,则方程cx2+bx+a=O有两个相等实数根.
其中正确的个数是( )
| A、O个 | B、l个 | C、2个 | D、3个 |
 如图,AD是△ABC的角平分线,∠C=90°,BC=9cm,BD=5cm,则点D到AB的距离是( )
如图,AD是△ABC的角平分线,∠C=90°,BC=9cm,BD=5cm,则点D到AB的距离是( )| A、4cm | B、5cm |
| C、6cm | D、9 cm |
已知:x+x-1=3,则x4+x-4的值为( )
| A、7 | B、49 | C、9 | D、47 |
 如图,把Rt△ABC绕点A逆时针旋转36°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=( )度.
如图,把Rt△ABC绕点A逆时针旋转36°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=( )度.| A、15 | B、18 | C、20 | D、30 |
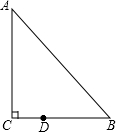 如图,Rt△ABC中,已知∠C=90°,∠B=48°,点D在边BC上,BD=2CD,把Rt△ABC绕点D逆时针旋转m(0°<m<180°)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=
如图,Rt△ABC中,已知∠C=90°,∠B=48°,点D在边BC上,BD=2CD,把Rt△ABC绕点D逆时针旋转m(0°<m<180°)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= 一段阶梯如图,其中∠C=90°,若高BC=5m,斜边AB=13m,若在梯子上铺上红地毯,则至少需要
一段阶梯如图,其中∠C=90°,若高BC=5m,斜边AB=13m,若在梯子上铺上红地毯,则至少需要